Menu Close

Question-14668

Tinku Tara 0 Comments
Pin




Question Number 14668 by tawa tawa last updated on 03/Jun/17
Commented by tawa tawa last updated on 03/Jun/17
please the two questions.
$$\mathrm{please}\:\mathrm{the}\:\mathrm{two}\:\mathrm{questions}. \\ $$
Commented by mrW1 last updated on 03/Jun/17
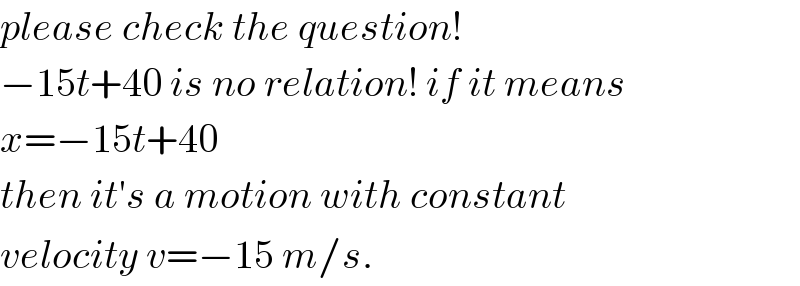
please check the question! −15t+40 is no relation! if it means x=−15t+40 then it′s a motion with constant velocity v=−15 m/s.
$${please}\:{check}\:{the}\:{question}!\: \\ $$$$−\mathrm{15}{t}+\mathrm{40}\:{is}\:{no}\:{relation}!\:{if}\:{it}\:{means} \\ $$$${x}=−\mathrm{15}{t}+\mathrm{40} \\ $$$${then}\:{it}'{s}\:{a}\:{motion}\:{with}\:{constant} \\ $$$${velocity}\:{v}=−\mathrm{15}\:{m}/{s}. \\ $$
Commented by tawa tawa last updated on 03/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by Tinkutara last updated on 03/Jun/17
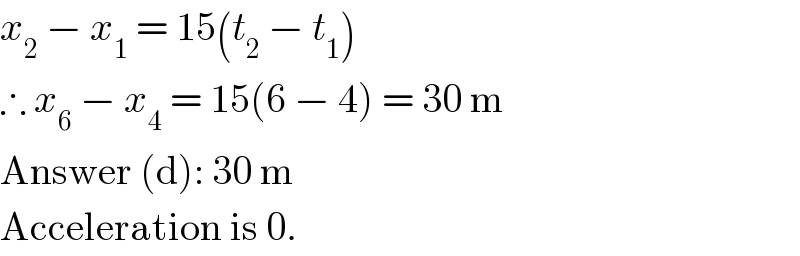
x_2 − x_1 = 15(t_2 − t_1 ) ∴ x_6 − x_4 = 15(6 − 4) = 30 m Answer (d): 30 m Acceleration is 0.
$${x}_{\mathrm{2}} \:−\:{x}_{\mathrm{1}} \:=\:\mathrm{15}\left({t}_{\mathrm{2}} \:−\:{t}_{\mathrm{1}} \right) \\ $$$$\therefore\:{x}_{\mathrm{6}} \:−\:{x}_{\mathrm{4}} \:=\:\mathrm{15}\left(\mathrm{6}\:−\:\mathrm{4}\right)\:=\:\mathrm{30}\:\mathrm{m} \\ $$$$\mathrm{Answer}\:\left(\mathrm{d}\right):\:\mathrm{30}\:\mathrm{m} \\ $$$$\mathrm{Acceleration}\:\mathrm{is}\:\mathrm{0}. \\ $$
Commented by tawa tawa last updated on 03/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mrW1 last updated on 03/Jun/17
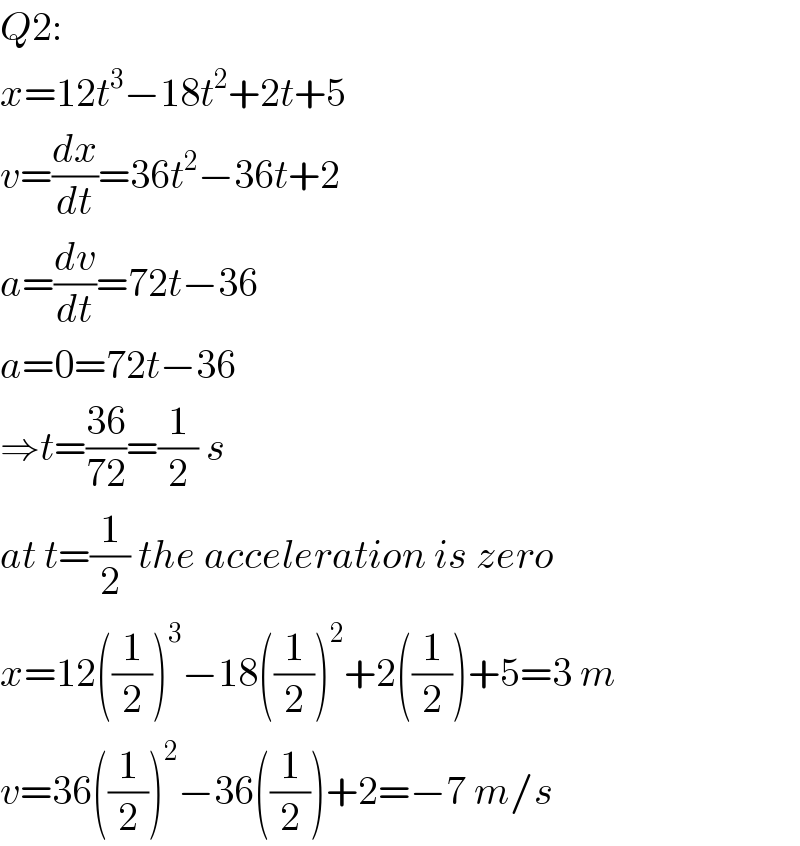
Q2: x=12t^3 −18t^2 +2t+5 v=(dx/dt)=36t^2 −36t+2 a=(dv/dt)=72t−36 a=0=72t−36 ⇒t=((36)/(72))=(1/2) s at t=(1/2) the acceleration is zero x=12((1/2))^3 −18((1/2))^2 +2((1/2))+5=3 m v=36((1/2))^2 −36((1/2))+2=−7 m/s
$${Q}\mathrm{2}: \\ $$$${x}=\mathrm{12}{t}^{\mathrm{3}} −\mathrm{18}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{5} \\ $$$${v}=\frac{{dx}}{{dt}}=\mathrm{36}{t}^{\mathrm{2}} −\mathrm{36}{t}+\mathrm{2} \\ $$$${a}=\frac{{dv}}{{dt}}=\mathrm{72}{t}−\mathrm{36} \\ $$$${a}=\mathrm{0}=\mathrm{72}{t}−\mathrm{36} \\ $$$$\Rightarrow{t}=\frac{\mathrm{36}}{\mathrm{72}}=\frac{\mathrm{1}}{\mathrm{2}}\:{s} \\ $$$${at}\:{t}=\frac{\mathrm{1}}{\mathrm{2}}\:{the}\:{acceleration}\:{is}\:{zero} \\ $$$${x}=\mathrm{12}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{18}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{5}=\mathrm{3}\:{m} \\ $$$${v}=\mathrm{36}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{36}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}=−\mathrm{7}\:{m}/{s} \\ $$
Commented by tawa tawa last updated on 03/Jun/17
Am really grateful sir. God bless you sir.
$$\mathrm{Am}\:\mathrm{really}\:\mathrm{grateful}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *