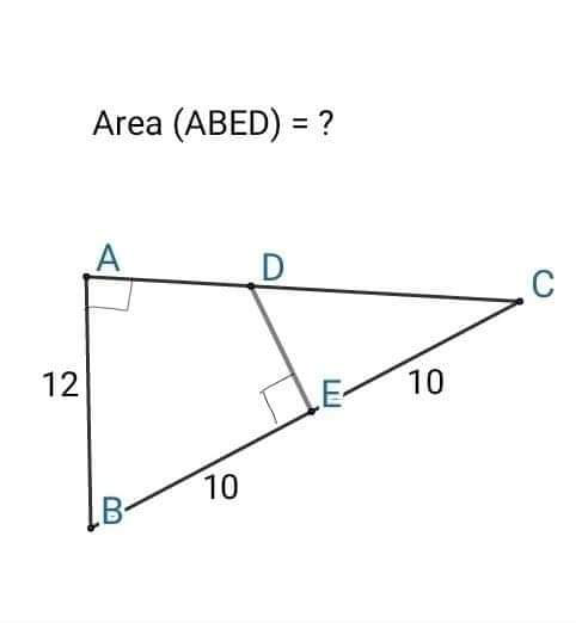
Question Number 146701 by bramlexs22 last updated on 15/Jul/21
Commented by bramlexs22 last updated on 15/Jul/21

$$\mathrm{how} \\ $$
Commented by som(math1967) last updated on 15/Jul/21

$$\mathrm{58}.\mathrm{5}{squnit} \\ $$
Answered by Rasheed.Sindhi last updated on 15/Jul/21

$$\bigtriangleup{ABC}: \\ $$$${sin}\angle{C}=\frac{\mathrm{12}}{\mathrm{20}}=\frac{\mathrm{3}}{\mathrm{5}}\Rightarrow\angle{C}=\mathrm{36}.\mathrm{87}° \\ $$$$\bigtriangleup{DCE}: \\ $$$${tan}\angle{C}=\frac{{DE}}{{EC}}\Rightarrow{DE}=\left({EC}\right){tan}\angle{C} \\ $$$${DE}=\mathrm{10}{tan}\mathrm{36}.\mathrm{87}=\mathrm{7}.\mathrm{5} \\ $$$$\bigtriangleup{BDE}: \\ $$$${BD}=\sqrt{\mathrm{10}^{\mathrm{2}} +\mathrm{7}.\mathrm{5}^{\mathrm{2}} }=\mathrm{12}.\mathrm{5} \\ $$$$\bigtriangleup{BDE}=\frac{\mathrm{1}}{\mathrm{2}}.{BE}.{DE}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{10}\right)\left(\mathrm{7}.\mathrm{5}\right)=\mathrm{37}.\mathrm{5} \\ $$$$\bigtriangleup{ABD}: \\ $$$${AD}=\sqrt{{BD}^{\mathrm{2}} −{AB}^{\mathrm{2}} }=\sqrt{\mathrm{12}.\mathrm{5}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }=\mathrm{3}.\mathrm{5} \\ $$$$\bigtriangleup{ABD}=\frac{\mathrm{1}}{\mathrm{2}}.{AB}.{AD}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{12}\right)\left(\mathrm{3}.\mathrm{5}\right)=\mathrm{21} \\ $$$${ABED}: \\ $$$${ABED}=\bigtriangleup{BDE}+\bigtriangleup{ABD}=\mathrm{37}.\mathrm{5}+\mathrm{21}=\mathrm{58}.\mathrm{5}\:{square}\:{units} \\ $$
Commented by bramlexs22 last updated on 15/Jul/21

$$\mathrm{yes}.\:\mathrm{i}'\mathrm{m}\:\mathrm{typo} \\ $$
Answered by som(math1967) last updated on 15/Jul/21

$${AC}=\sqrt{\mathrm{20}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }=\mathrm{16} \\ $$$${ar}.\bigtriangleup{ABC}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{12}×\mathrm{16}=\mathrm{96}{squnit} \\ $$$$\bigtriangleup{DEC}\sim\bigtriangleup{BAC} \\ $$$$\therefore\frac{{DE}}{{AB}}=\frac{{CE}}{{AC}} \\ $$$${DE}=\mathrm{12}×\frac{\mathrm{10}}{\mathrm{16}}=\frac{\mathrm{15}}{\mathrm{2}}=\mathrm{7}.\mathrm{5} \\ $$$${Ar}\bigtriangleup{CDE}=\frac{\mathrm{1}}{\mathrm{2}}×{CE}×{DE}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{10}×\mathrm{7}.\mathrm{5}=\mathrm{37}.\mathrm{5}{squnit} \\ $$$${Ar}\:{ABED}=\mathrm{96}−\mathrm{37}.\mathrm{5}=\mathrm{58}.\mathrm{5}{squnit} \\ $$
Commented by Rasheed.Sindhi last updated on 15/Jul/21

$$\mathcal{N}{ice}! \\ $$
Commented by otchereabdullai@gmail.com last updated on 16/Jul/21

$$\mathrm{nice}\:\mathrm{one}\:\mathrm{sir}! \\ $$
Commented by som(math1967) last updated on 16/Jul/21

$${Thank}\:{you} \\ $$
Answered by bramlexs22 last updated on 15/Jul/21

$$\mathrm{from}\:\angle\mathrm{C}\::\:\mathrm{sin}\:\mathrm{C}=\mathrm{sin}\:\mathrm{C} \\ $$$$\Rightarrow\frac{\mathrm{DE}}{\:\sqrt{\mathrm{100}+\mathrm{DE}^{\mathrm{2}} }}\:=\:\frac{\mathrm{12}}{\mathrm{20}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{25DE}^{\mathrm{2}} =\mathrm{900}+\mathrm{9DE}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{DE}=\sqrt{\frac{\mathrm{900}}{\mathrm{16}}}\:=\:\frac{\mathrm{30}}{\mathrm{4}}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\mathrm{C}=\mathrm{tan}\:\mathrm{C} \\ $$$$\Rightarrow\frac{\mathrm{12}}{\mathrm{AC}}=\frac{\frac{\mathrm{15}}{\mathrm{2}}}{\mathrm{10}}\:\Rightarrow\frac{\mathrm{12}}{\mathrm{AC}}=\frac{\cancel{\mathrm{15}}\:^{\mathrm{3}} }{\cancel{\mathrm{20}}\:^{\mathrm{4}} } \\ $$$$\Rightarrow\mathrm{AC}\:=\:\mathrm{16}\: \\ $$$$\mathrm{Area}\:\mathrm{ABED}\:=\:\mathrm{area}\:\mathrm{ABC}−\mathrm{area}\:\mathrm{CED} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{12}×\mathrm{16}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{15}}{\mathrm{2}}×\mathrm{10} \\ $$$$\:=\:\mathrm{96}−\frac{\mathrm{75}}{\mathrm{2}}=\frac{\mathrm{192}−\mathrm{75}}{\mathrm{2}}\:=\:\frac{\mathrm{117}}{\mathrm{2}} \\ $$$$\:=\:\mathrm{58}.\mathrm{5}\: \\ $$
