Question Number 146730 by puissant last updated on 15/Jul/21

Commented by puissant last updated on 15/Jul/21

$$\mathrm{merci} \\ $$
Commented by Olaf_Thorendsen last updated on 15/Jul/21
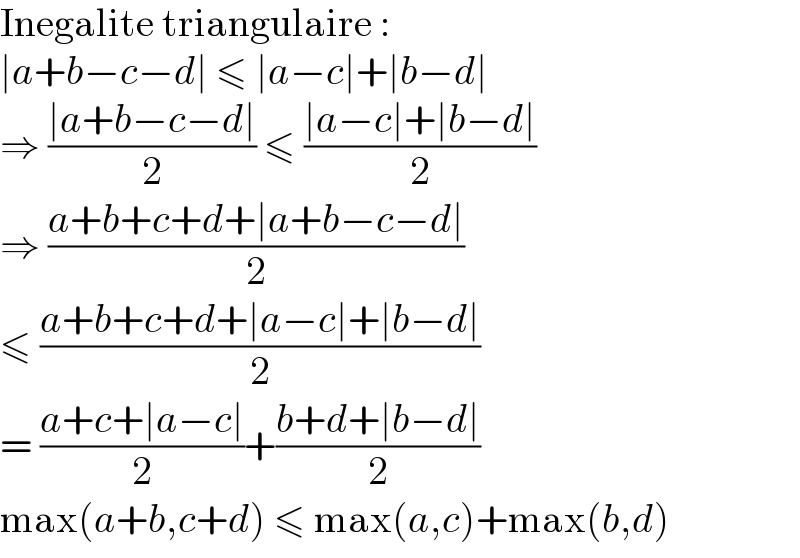
$$\mathrm{Inegalite}\:\mathrm{triangulaire}\:: \\ $$$$\mid{a}+{b}−{c}−{d}\mid\:\leqslant\:\mid{a}−{c}\mid+\mid{b}−{d}\mid \\ $$$$\Rightarrow\:\frac{\mid{a}+{b}−{c}−{d}\mid}{\mathrm{2}}\:\leqslant\:\frac{\mid{a}−{c}\mid+\mid{b}−{d}\mid}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{a}+{b}+{c}+{d}+\mid{a}+{b}−{c}−{d}\mid}{\mathrm{2}} \\ $$$$\leqslant\:\frac{{a}+{b}+{c}+{d}+\mid{a}−{c}\mid+\mid{b}−{d}\mid}{\mathrm{2}} \\ $$$$=\:\frac{{a}+{c}+\mid{a}−{c}\mid}{\mathrm{2}}+\frac{{b}+{d}+\mid{b}−{d}\mid}{\mathrm{2}} \\ $$$$\mathrm{max}\left({a}+{b},{c}+{d}\right)\:\leqslant\:\mathrm{max}\left({a},{c}\right)+\mathrm{max}\left({b},{d}\right) \\ $$
Answered by Olaf_Thorendsen last updated on 15/Jul/21

$$\mathrm{Differentes}\:\mathrm{approches}\:\mathrm{mais}\:\mathrm{une}\: \\ $$$$\mathrm{approche}\:\mathrm{elegante}\:\mathrm{consiste}\:\mathrm{a}\:\mathrm{remarquer} \\ $$$$\mathrm{que}\:\mathrm{max}\left({x},{y}\right)\:=\:\frac{{x}+{y}+\mid{x}−{y}\mid}{\mathrm{2}}. \\ $$$$\mathrm{Il}\:\mathrm{ne}\:\mathrm{reste}\:\mathrm{alors}\:\mathrm{qu}'\mathrm{a}\:\mathrm{utiliser} \\ $$$$\mathrm{l}'\mathrm{inegalite}\:\mathrm{triangulaire}. \\ $$
