Question Number 146824 by alcohol last updated on 16/Jul/21
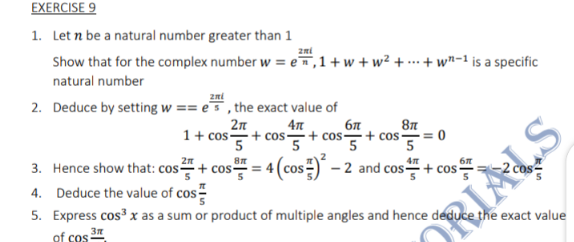
Answered by Olaf_Thorendsen last updated on 16/Jul/21
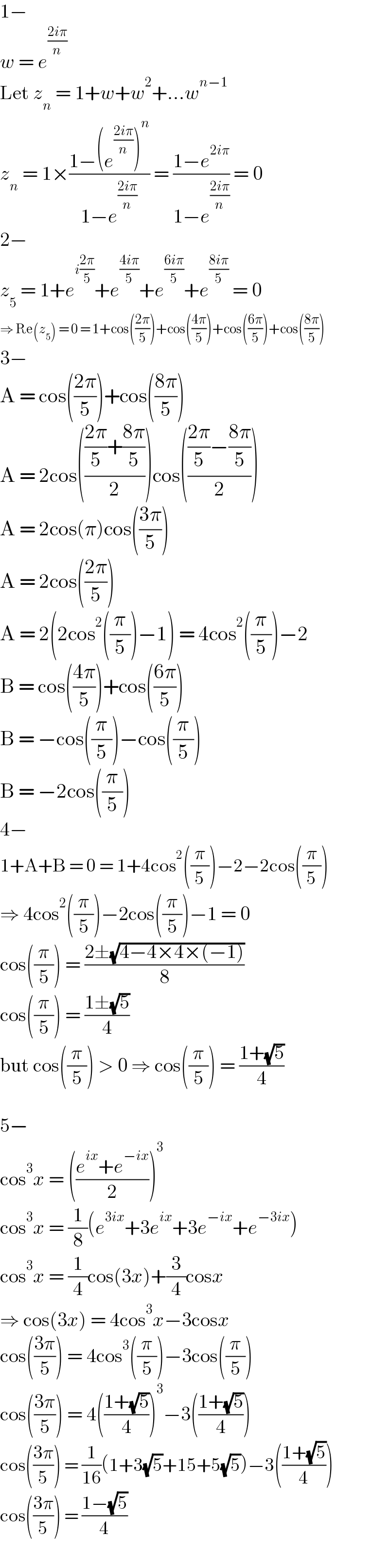
$$\mathrm{1}− \\ $$$${w}\:=\:{e}^{\frac{\mathrm{2}{i}\pi}{{n}}} \\ $$$$\mathrm{Let}\:{z}_{{n}} \:=\:\mathrm{1}+{w}+{w}^{\mathrm{2}} +…{w}^{{n}−\mathrm{1}} \\ $$$${z}_{{n}} \:=\:\mathrm{1}×\frac{\mathrm{1}−\left({e}^{\frac{\mathrm{2}{i}\pi}{{n}}} \right)^{{n}} }{\mathrm{1}−{e}^{\frac{\mathrm{2}{i}\pi}{{n}}} }\:=\:\frac{\mathrm{1}−{e}^{\mathrm{2}{i}\pi} }{\mathrm{1}−{e}^{\frac{\mathrm{2}{i}\pi}{{n}}} }\:=\:\mathrm{0} \\ $$$$\mathrm{2}− \\ $$$${z}_{\mathrm{5}} \:=\:\mathrm{1}+{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{5}}} +{e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{5}}} +{e}^{\frac{\mathrm{6}{i}\pi}{\mathrm{5}}} +{e}^{\frac{\mathrm{8}{i}\pi}{\mathrm{5}}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{Re}\left({z}_{\mathrm{5}} \right)\:=\:\mathrm{0}\:=\:\mathrm{1}+\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right)+\mathrm{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{5}}\right)+\mathrm{cos}\left(\frac{\mathrm{6}\pi}{\mathrm{5}}\right)+\mathrm{cos}\left(\frac{\mathrm{8}\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{3}− \\ $$$$\mathrm{A}\:=\:\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right)+\mathrm{cos}\left(\frac{\mathrm{8}\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{A}\:=\:\mathrm{2cos}\left(\frac{\frac{\mathrm{2}\pi}{\mathrm{5}}+\frac{\mathrm{8}\pi}{\mathrm{5}}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\frac{\mathrm{2}\pi}{\mathrm{5}}−\frac{\mathrm{8}\pi}{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\mathrm{A}\:=\:\mathrm{2cos}\left(\pi\right)\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{A}\:=\:\mathrm{2cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{A}\:=\:\mathrm{2}\left(\mathrm{2cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right)−\mathrm{1}\right)\:=\:\mathrm{4cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right)−\mathrm{2} \\ $$$$\mathrm{B}\:=\:\mathrm{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{5}}\right)+\mathrm{cos}\left(\frac{\mathrm{6}\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{B}\:=\:−\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)−\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{B}\:=\:−\mathrm{2cos}\left(\frac{\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{4}− \\ $$$$\mathrm{1}+\mathrm{A}+\mathrm{B}\:=\:\mathrm{0}\:=\:\mathrm{1}+\mathrm{4cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right)−\mathrm{2}−\mathrm{2cos}\left(\frac{\pi}{\mathrm{5}}\right) \\ $$$$\Rightarrow\:\mathrm{4cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right)−\mathrm{2cos}\left(\frac{\pi}{\mathrm{5}}\right)−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)\:=\:\frac{\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}×\mathrm{4}×\left(−\mathrm{1}\right)}}{\mathrm{8}} \\ $$$$\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)\:=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{but}\:\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)\:>\:\mathrm{0}\:\Rightarrow\:\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\: \\ $$$$\mathrm{5}− \\ $$$$\mathrm{cos}^{\mathrm{3}} {x}\:=\:\left(\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\mathrm{cos}^{\mathrm{3}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left({e}^{\mathrm{3}{ix}} +\mathrm{3}{e}^{{ix}} +\mathrm{3}{e}^{−{ix}} +{e}^{−\mathrm{3}{ix}} \right) \\ $$$$\mathrm{cos}^{\mathrm{3}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{3}{x}\right)+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}{x} \\ $$$$\Rightarrow\:\mathrm{cos}\left(\mathrm{3}{x}\right)\:=\:\mathrm{4cos}^{\mathrm{3}} {x}−\mathrm{3cos}{x} \\ $$$$\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right)\:=\:\mathrm{4cos}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{5}}\right)−\mathrm{3cos}\left(\frac{\pi}{\mathrm{5}}\right) \\ $$$$\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right)\:=\:\mathrm{4}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{3}} −\mathrm{3}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right) \\ $$$$\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}+\mathrm{3}\sqrt{\mathrm{5}}+\mathrm{15}+\mathrm{5}\sqrt{\mathrm{5}}\right)−\mathrm{3}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right) \\ $$$$\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right)\:=\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$
