Question Number 146960 by mathdanisur last updated on 16/Jul/21

Answered by TheHoneyCat last updated on 16/Jul/21
![let A be the fuction that gives the area of a surface let Δ=ABO let x be the hatched area let D be the intersection between [AO] and the circle C(O,OR) let y be the portion AOD of the circle A(y)=πBC((180−90−A^Λ )/(360)) A(ABO)=(√(BC^2 −(((BC)/2))^2 ))=BC((√3)/2) A(x)=A(ABO)−A(y) A(x)=BC(((√3)/2)−π((180−90−A^Λ )/(360)))_■ I let you plot that on your calculator if you want a value by the way: you gave one information without necessity, indeed: A^Λ =30° can be deduced from the fact that AO=2BO ;−)](https://www.tinkutara.com/question/Q146972.png)
$$\mathrm{let}\:\mathscr{A}\:\mathrm{be}\:\mathrm{the}\:\mathrm{fuction}\:\mathrm{that}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{surface} \\ $$$$\mathrm{let}\:\Delta={ABO} \\ $$$$\mathrm{let}\:{x}\:\mathrm{be}\:\mathrm{the}\:\mathrm{hatched}\:\mathrm{area} \\ $$$$\mathrm{let}\:{D}\:\mathrm{be}\:\mathrm{the}\:\mathrm{intersection}\:\mathrm{between}\:\left[\mathrm{AO}\right]\:\mathrm{and}\:\mathrm{the}\:\mathrm{circle}\:\mathscr{C}\left({O},{OR}\right) \\ $$$$\mathrm{let}\:{y}\:\mathrm{be}\:\mathrm{the}\:\mathrm{portion}\:{AOD}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$$ \\ $$$$\mathscr{A}\left({y}\right)=\pi{BC}\frac{\mathrm{180}−\mathrm{90}−\overset{\Lambda} {{A}}}{\mathrm{360}} \\ $$$$\mathscr{A}\left({ABO}\right)=\sqrt{{BC}^{\mathrm{2}} −\left(\frac{{BC}}{\mathrm{2}}\right)^{\mathrm{2}} }={BC}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathscr{A}\left({x}\right)=\mathscr{A}\left({ABO}\right)−\mathscr{A}\left({y}\right) \\ $$$$\mathscr{A}\left({x}\right)={BC}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\pi\frac{\mathrm{180}−\mathrm{90}−\overset{\Lambda} {{A}}}{\mathrm{360}}\right)_{\blacksquare} \\ $$$$ \\ $$$${I}\:{let}\:{you}\:{plot}\:{that}\:{on}\:{your}\:{calculator}\:{if}\:{you}\:{want}\:{a}\:{value} \\ $$$${by}\:{the}\:{way}:\:{you}\:{gave}\:{one}\:{information}\:{without}\:{necessity}, \\ $$$${indeed}:\:\overset{\Lambda} {{A}}=\mathrm{30}°\:{can}\:{be}\:{deduced}\:{from}\:{the}\:{fact}\:{that}\:{AO}=\mathrm{2}{BO} \\ $$$$\left.;−\right) \\ $$$$ \\ $$
Commented by mathdanisur last updated on 16/Jul/21

$${thanks}\:{Ser}\:{but}\:{answer}? \\ $$
Answered by ajfour last updated on 16/Jul/21
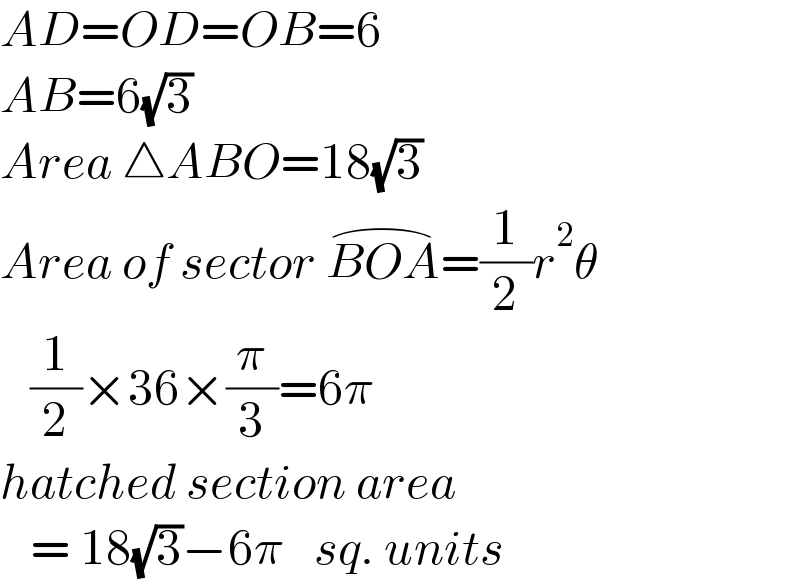
$${AD}={OD}={OB}=\mathrm{6} \\ $$$${AB}=\mathrm{6}\sqrt{\mathrm{3}} \\ $$$${Area}\:\bigtriangleup{ABO}=\mathrm{18}\sqrt{\mathrm{3}} \\ $$$${Area}\:{of}\:{sector}\:\overset{\frown} {{BOA}}=\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \theta \\ $$$$\:\:\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{36}×\frac{\pi}{\mathrm{3}}=\mathrm{6}\pi \\ $$$${hatched}\:{section}\:{area} \\ $$$$\:\:\:=\:\mathrm{18}\sqrt{\mathrm{3}}−\mathrm{6}\pi\:\:\:{sq}.\:{units} \\ $$
Commented by mathdanisur last updated on 17/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
