Question Number 146962 by Sameza last updated on 16/Jul/21

Answered by Olaf_Thorendsen last updated on 16/Jul/21
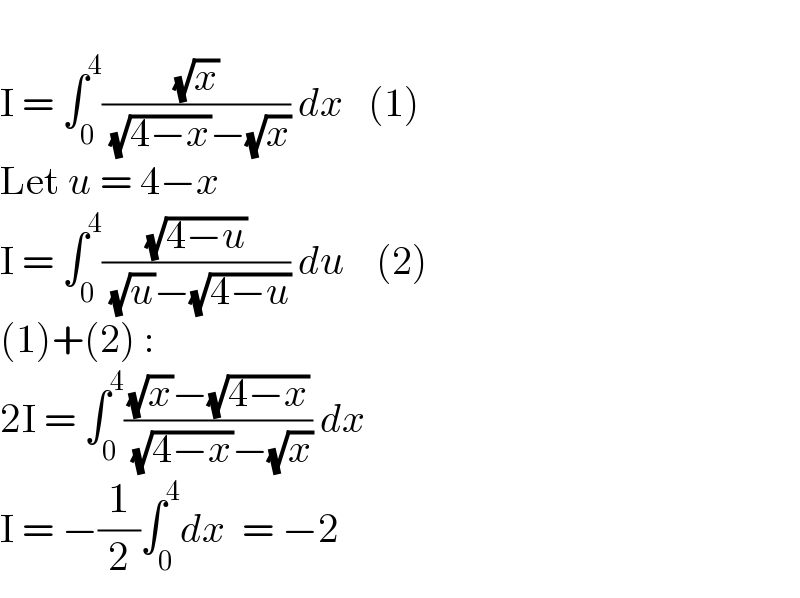
$$ \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\sqrt{{x}}}{\:\sqrt{\mathrm{4}−{x}}−\sqrt{{x}}}\:{dx}\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{4}−{x} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\sqrt{\mathrm{4}−{u}}}{\:\sqrt{{u}}−\sqrt{\mathrm{4}−{u}}}\:{du}\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:: \\ $$$$\mathrm{2I}\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\sqrt{{x}}−\sqrt{\mathrm{4}−{x}}}{\:\sqrt{\mathrm{4}−{x}}−\sqrt{{x}}}\:{dx} \\ $$$$\mathrm{I}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{4}} {dx}\:\:=\:−\mathrm{2} \\ $$
