Question Number 14701 by tawa tawa last updated on 03/Jun/17

Commented by mrW1 last updated on 03/Jun/17

$${I}\:{think}\:{none}\:{of}\:{the}\:{answers}\:{is}\:{right}. \\ $$$${xy}=\mathrm{20}^{\mathrm{1}} =\mathrm{20} \\ $$$${x}+{y}=\mathrm{5}^{\mathrm{2}} =\mathrm{25} \\ $$$${x}^{\mathrm{2}} −\mathrm{25}{x}+\mathrm{20}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{25}\pm\sqrt{\mathrm{545}}}{\mathrm{2}} \\ $$$${y}=\frac{−\mathrm{25}\mp\sqrt{\mathrm{545}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {y}={xy}×{x}=\mathrm{20}{x}=\mathrm{10}\left(\mathrm{25}\pm\sqrt{\mathrm{545}}\right) \\ $$
Commented by tawa tawa last updated on 03/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
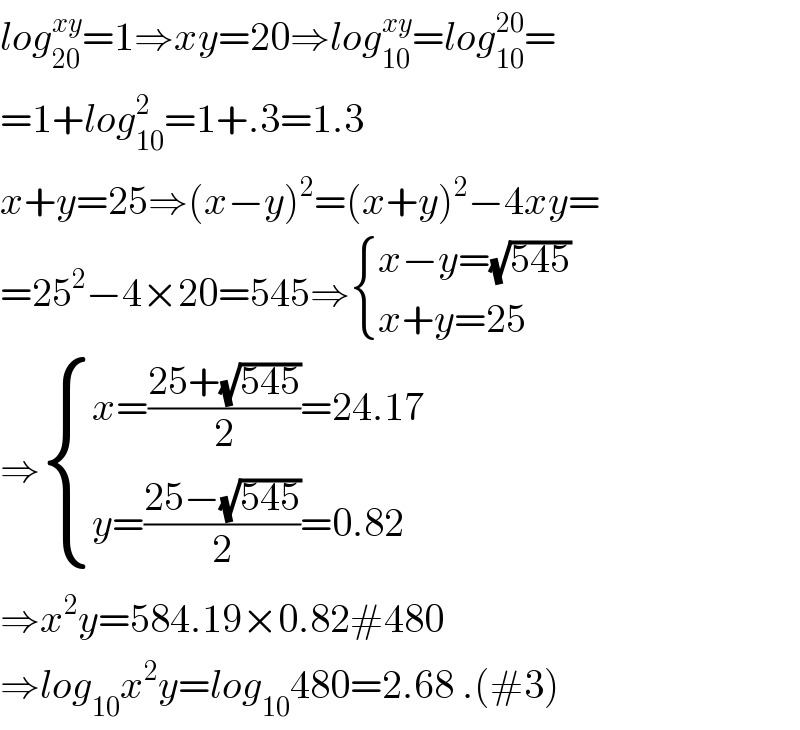
$${log}_{\mathrm{20}} ^{{xy}} =\mathrm{1}\Rightarrow{xy}=\mathrm{20}\Rightarrow{log}_{\mathrm{10}} ^{{xy}} ={log}_{\mathrm{10}} ^{\mathrm{20}} = \\ $$$$=\mathrm{1}+{log}_{\mathrm{10}} ^{\mathrm{2}} =\mathrm{1}+.\mathrm{3}=\mathrm{1}.\mathrm{3} \\ $$$${x}+{y}=\mathrm{25}\Rightarrow\left({x}−{y}\right)^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}= \\ $$$$=\mathrm{25}^{\mathrm{2}} −\mathrm{4}×\mathrm{20}=\mathrm{545}\Rightarrow\begin{cases}{{x}−{y}=\sqrt{\mathrm{545}}}\\{{x}+{y}=\mathrm{25}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{{x}=\frac{\mathrm{25}+\sqrt{\mathrm{545}}}{\mathrm{2}}=\mathrm{24}.\mathrm{17}}\\{{y}=\frac{\mathrm{25}−\sqrt{\mathrm{545}}}{\mathrm{2}}=\mathrm{0}.\mathrm{82}}\end{cases} \\ $$$$\Rightarrow{x}^{\mathrm{2}} {y}=\mathrm{584}.\mathrm{19}×\mathrm{0}.\mathrm{82}#\mathrm{480} \\ $$$$\Rightarrow{log}_{\mathrm{10}} {x}^{\mathrm{2}} {y}={log}_{\mathrm{10}} \mathrm{480}=\mathrm{2}.\mathrm{68}\:.\left(#\mathrm{3}\right) \\ $$
Commented by tawa tawa last updated on 04/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 04/Jun/17
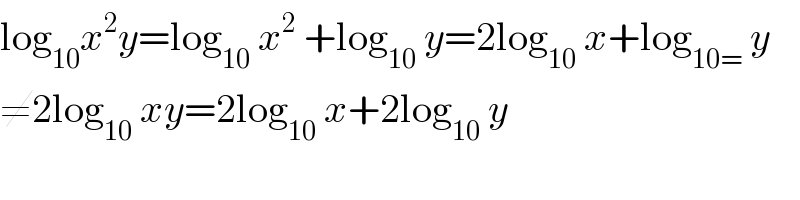
$$\mathrm{log}_{\mathrm{10}} {x}^{\mathrm{2}} {y}=\mathrm{log}_{\mathrm{10}} \:{x}^{\mathrm{2}} \:+\mathrm{log}_{\mathrm{10}} \:{y}=\mathrm{2log}_{\mathrm{10}} \:{x}+\mathrm{log}_{\mathrm{10}=} \:{y} \\ $$$$\neq\mathrm{2log}_{\mathrm{10}} \:{xy}=\mathrm{2log}_{\mathrm{10}} \:{x}+\mathrm{2log}_{\mathrm{10}} \:{y} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
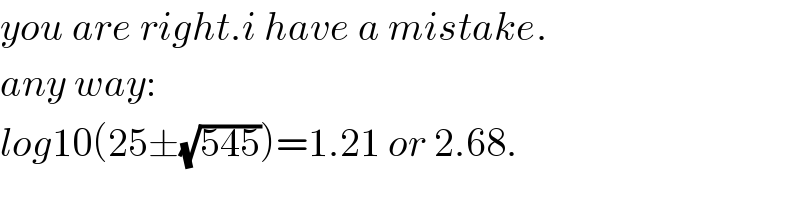
$${you}\:{are}\:{right}.{i}\:{have}\:{a}\:{mistake}. \\ $$$${any}\:{way}: \\ $$$${log}\mathrm{10}\left(\mathrm{25}\pm\sqrt{\mathrm{545}}\right)=\mathrm{1}.\mathrm{21}\:{or}\:\mathrm{2}.\mathrm{68}. \\ $$
