Question Number 147031 by mnjuly1970 last updated on 17/Jul/21

Answered by mindispower last updated on 17/Jul/21
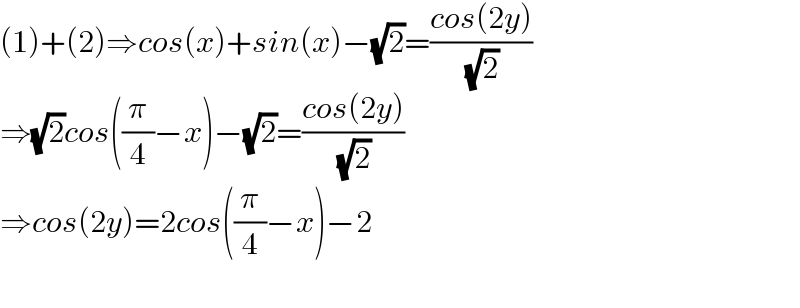
$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow{cos}\left({x}\right)+{sin}\left({x}\right)−\sqrt{\mathrm{2}}=\frac{{cos}\left(\mathrm{2}{y}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)−\sqrt{\mathrm{2}}=\frac{{cos}\left(\mathrm{2}{y}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{cos}\left(\mathrm{2}{y}\right)=\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)−\mathrm{2} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 17/Jul/21

$${thanks}\:{alot} \\ $$
Answered by gsk2684 last updated on 17/Jul/21
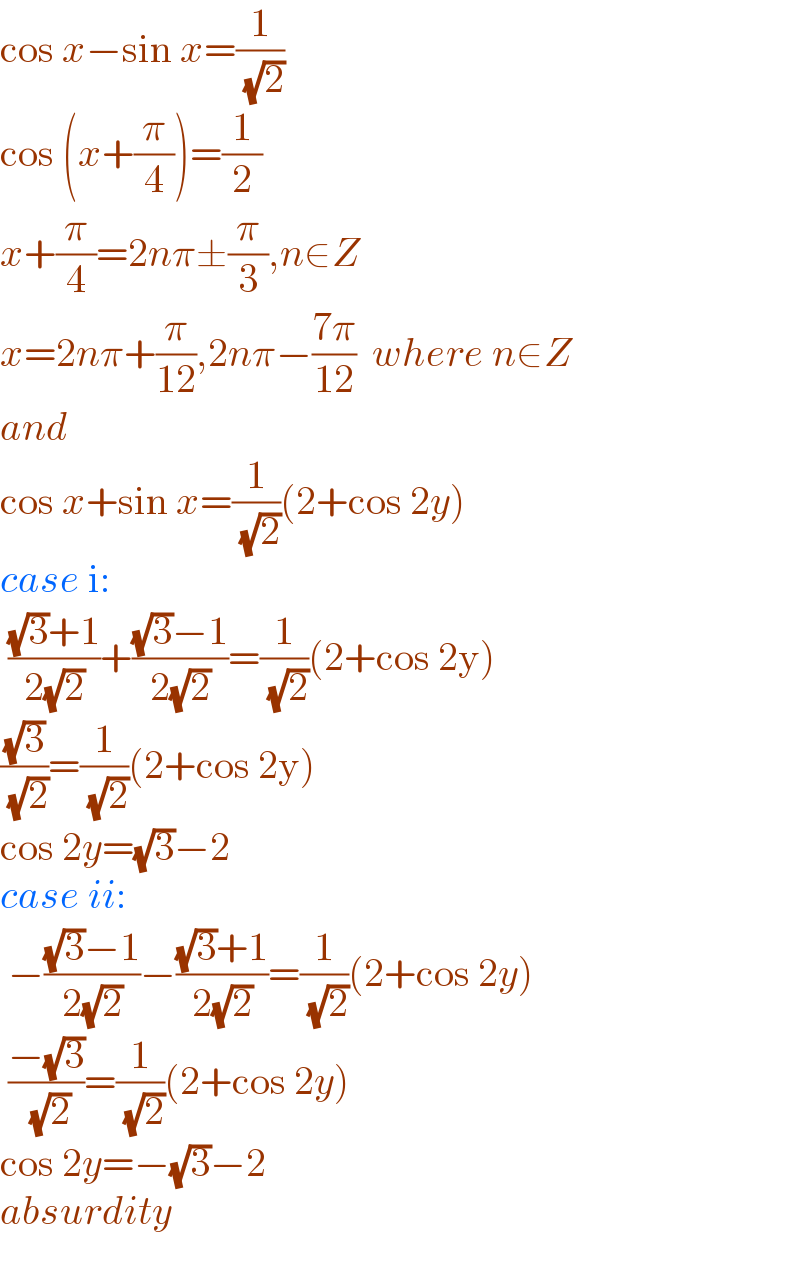
$$\mathrm{cos}\:{x}−\mathrm{sin}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}+\frac{\pi}{\mathrm{4}}=\mathrm{2}{n}\pi\pm\frac{\pi}{\mathrm{3}},{n}\in{Z} \\ $$$${x}=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{12}},\mathrm{2}{n}\pi−\frac{\mathrm{7}\pi}{\mathrm{12}}\:\:{where}\:{n}\in{Z} \\ $$$${and}\: \\ $$$$\mathrm{cos}\:{x}+\mathrm{sin}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{2}{y}\right) \\ $$$${case}\:\mathrm{i}: \\ $$$$\:\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{2y}\right) \\ $$$$\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{2y}\right) \\ $$$$\mathrm{cos}\:\mathrm{2}{y}=\sqrt{\mathrm{3}}−\mathrm{2} \\ $$$${case}\:{ii}: \\ $$$$\:−\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}−\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{2}{y}\right) \\ $$$$\:\frac{−\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{2}{y}\right) \\ $$$$\mathrm{cos}\:\mathrm{2}{y}=−\sqrt{\mathrm{3}}−\mathrm{2} \\ $$$${absurdity} \\ $$
Commented by mnjuly1970 last updated on 17/Jul/21

$${grateful}\:… \\ $$
Answered by mr W last updated on 17/Jul/21

$$\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{cos}\:{x}−\mathrm{sin}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{cos}\:{x}+\mathrm{sin}\:{x}=\frac{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{y}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{cos}\:{x}=\frac{\mathrm{3}+\mathrm{cos}\:\mathrm{2}{y}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{y}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\left(\frac{\mathrm{3}+\mathrm{cos}\:\mathrm{2}{y}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{y}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{y}+\mathrm{4cos}\:\mathrm{2}{y}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{2}{y}=\frac{−\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{2}+\sqrt{\mathrm{3}},−\mathrm{2}−\sqrt{\mathrm{3}}\:\left({rejected}\right) \\ $$
Commented by mnjuly1970 last updated on 17/Jul/21

$$\:{thx}\:{mr}\:\mathrm{W} \\ $$
Answered by EDWIN88 last updated on 17/Jul/21
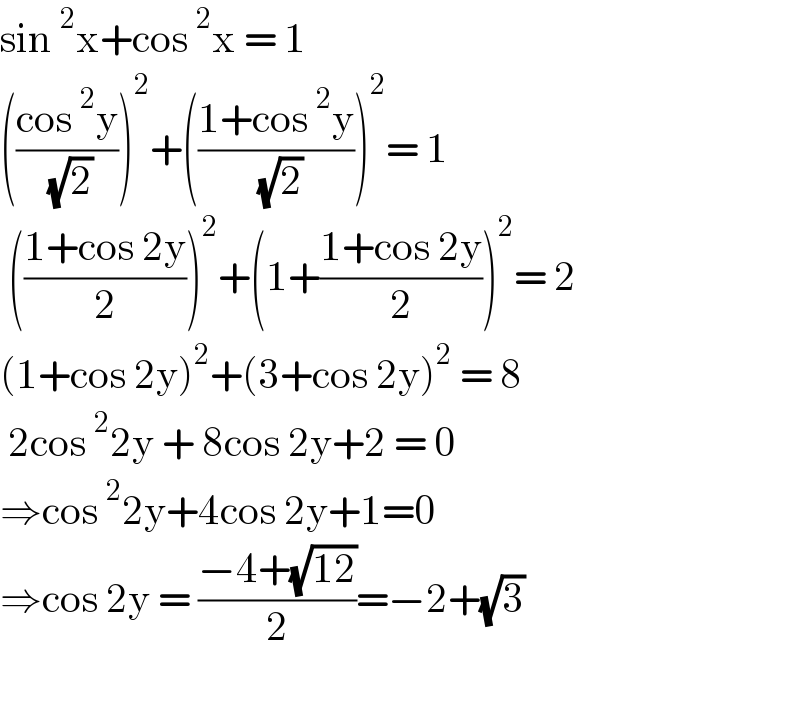
$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{1} \\ $$$$\left(\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{y}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{y}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\:\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2y}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{1}+\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2y}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{2} \\ $$$$\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2y}\right)^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{cos}\:\mathrm{2y}\right)^{\mathrm{2}} \:=\:\mathrm{8} \\ $$$$\:\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2y}\:+\:\mathrm{8cos}\:\mathrm{2y}+\mathrm{2}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}} \mathrm{2y}+\mathrm{4cos}\:\mathrm{2y}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2y}\:=\:\frac{−\mathrm{4}+\sqrt{\mathrm{12}}}{\mathrm{2}}=−\mathrm{2}+\sqrt{\mathrm{3}}\: \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 17/Jul/21
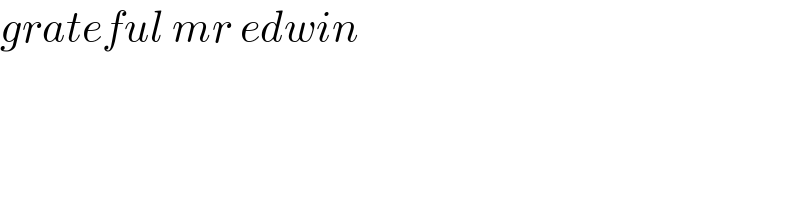
$${grateful}\:{mr}\:{edwin} \\ $$
Answered by behi834171 last updated on 17/Jul/21
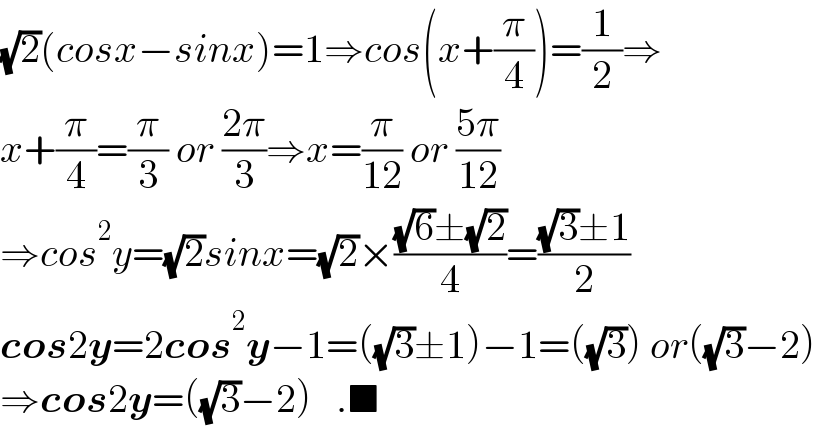
$$\sqrt{\mathrm{2}}\left({cosx}−{sinx}\right)=\mathrm{1}\Rightarrow{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow \\ $$$${x}+\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{3}}\:{or}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\Rightarrow{x}=\frac{\pi}{\mathrm{12}}\:{or}\:\frac{\mathrm{5}\pi}{\mathrm{12}} \\ $$$$\Rightarrow{cos}^{\mathrm{2}} {y}=\sqrt{\mathrm{2}}{sinx}=\sqrt{\mathrm{2}}×\frac{\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}\pm\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{y}}=\mathrm{2}\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{y}}−\mathrm{1}=\left(\sqrt{\mathrm{3}}\pm\mathrm{1}\right)−\mathrm{1}=\left(\sqrt{\mathrm{3}}\right)\:{or}\left(\sqrt{\mathrm{3}}−\mathrm{2}\right) \\ $$$$\Rightarrow\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{y}}=\left(\sqrt{\mathrm{3}}−\mathrm{2}\right)\:\:\:.\blacksquare \\ $$
