Question Number 147162 by nadovic last updated on 18/Jul/21

Answered by liberty last updated on 18/Jul/21
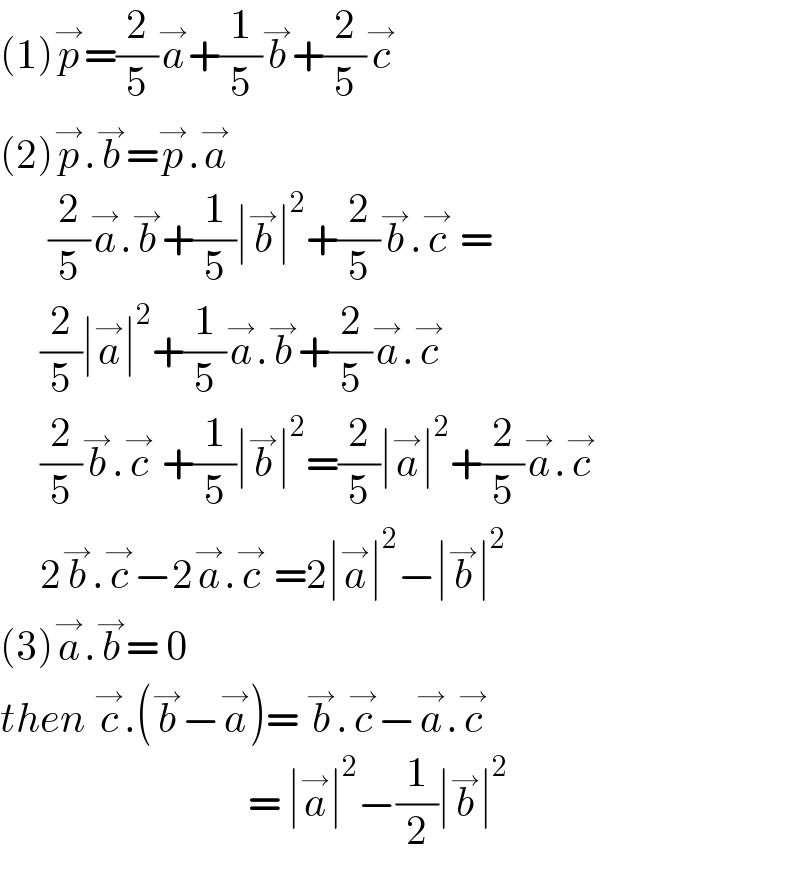
$$\left(\mathrm{1}\right)\overset{\rightarrow} {{p}}=\frac{\mathrm{2}}{\mathrm{5}}\overset{\rightarrow} {{a}}+\frac{\mathrm{1}}{\mathrm{5}}\overset{\rightarrow} {{b}}+\frac{\mathrm{2}}{\mathrm{5}}\overset{\rightarrow} {{c}} \\ $$$$\left(\mathrm{2}\right)\overset{\rightarrow} {{p}}.\overset{\rightarrow} {{b}}=\overset{\rightarrow} {{p}}.\overset{\rightarrow} {{a}} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}+\frac{\mathrm{1}}{\mathrm{5}}\mid\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{5}}\overset{\rightarrow} {{b}}.\overset{\rightarrow} {{c}}\:= \\ $$$$\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{5}}\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}+\frac{\mathrm{2}}{\mathrm{5}}\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}} \\ $$$$\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}\overset{\rightarrow} {{b}}.\overset{\rightarrow} {{c}}\:+\frac{\mathrm{1}}{\mathrm{5}}\mid\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{5}}\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{5}}\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}} \\ $$$$\:\:\:\:\:\mathrm{2}\overset{\rightarrow} {{b}}.\overset{\rightarrow} {{c}}−\mathrm{2}\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}}\:=\mathrm{2}\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} −\mid\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}=\:\mathrm{0} \\ $$$${then}\:\overset{\rightarrow} {{c}}.\left(\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{a}}\right)=\:\overset{\rightarrow} {{b}}.\overset{\rightarrow} {{c}}−\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mid\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} \\ $$
Commented by nadovic last updated on 18/Jul/21
$${Thank}\:{you}\:{very}\:{much}\:{Sir} \\ $$
