Question Number 14719 by Abbas-Nahi last updated on 03/Jun/17
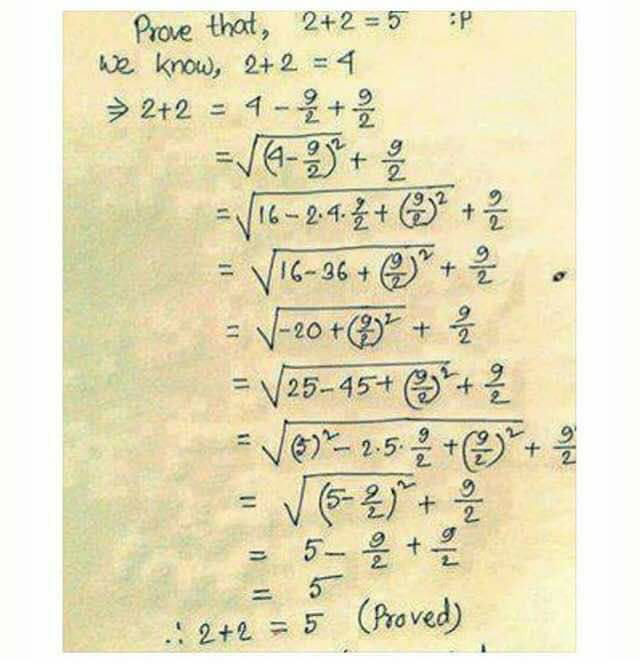
Commented by Abbas-Nahi last updated on 03/Jun/17

$${Is}\:{the}\:{solution}\:{possible}\:{mathmatically} \\ $$$${orNOT}\:{and}\:{whether}\:{it}\:{is}\:{logical}\:{or}\:{not} \\ $$$$ \\ $$
Commented by Abbas-Nahi last updated on 03/Jun/17

$${really}\:{want}\:{to}\:{help}? \\ $$
Commented by mrW1 last updated on 04/Jun/17

$$\mathrm{4}−\frac{\mathrm{9}}{\mathrm{2}}\neq\sqrt{\left(\mathrm{4}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{4}−\frac{\mathrm{9}}{\mathrm{2}}=−\sqrt{\left(\mathrm{4}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} }=−\sqrt{\left(\mathrm{5}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} }=−\left(\mathrm{5}−\frac{\mathrm{9}}{\mathrm{2}}\right) \\ $$
Commented by mrW1 last updated on 04/Jun/17
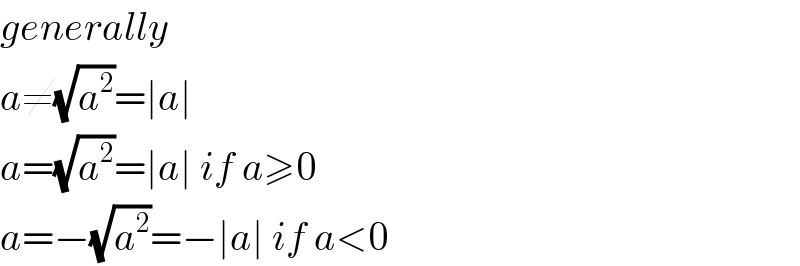
$${generally} \\ $$$${a}\neq\sqrt{{a}^{\mathrm{2}} }=\mid{a}\mid \\ $$$${a}=\sqrt{{a}^{\mathrm{2}} }=\mid{a}\mid\:{if}\:{a}\geqslant\mathrm{0} \\ $$$${a}=−\sqrt{{a}^{\mathrm{2}} }=−\mid{a}\mid\:{if}\:{a}<\mathrm{0} \\ $$
Commented by RasheedSoomro last updated on 04/Jun/17

$${a}=\sqrt{{a}^{\mathrm{2}} }={a}\:{if}\:{a}\geqslant\mathrm{0} \\ $$$${a}=−\sqrt{{a}^{\mathrm{2}} }=−{a}\:{if}\:{a}<\mathrm{0} \\ $$$$\mathrm{No}\:\mathrm{need}\:\mathrm{to}\:\mathrm{use}\:\:\:\mid\:\:\:\:\mid \\ $$$$\mathrm{Am}\:\mathrm{I}\:\mathrm{right}? \\ $$
Commented by Tinkutara last updated on 04/Jun/17

$$\mathrm{Yes},\:\mathrm{in}\:\mathrm{my}\:\mathrm{opinion}. \\ $$
Commented by mrW1 last updated on 04/Jun/17

$${you}\:{are}\:{right}\:{sir}.\:{I}\:{just}\:{want}\:{to}\:{say}\:\sqrt{{a}^{\mathrm{2}} } \\ $$$${is}\:{only}\:{the}\:{absolute}\:{value}\:{of}\:{a}\:{number}, \\ $$$${but}\:{not}\:{always}\:{the}\:{number}\:{itself}. \\ $$
Commented by Abbas-Nahi last updated on 04/Jun/17

$${thank}\:{you}\:{for}\:{your}\:{cooperation}\:{with} \\ $$$${my}\:{best}\:{regards} \\ $$
