Question Number 147252 by mathlove last updated on 19/Jul/21

Answered by Olaf_Thorendsen last updated on 19/Jul/21
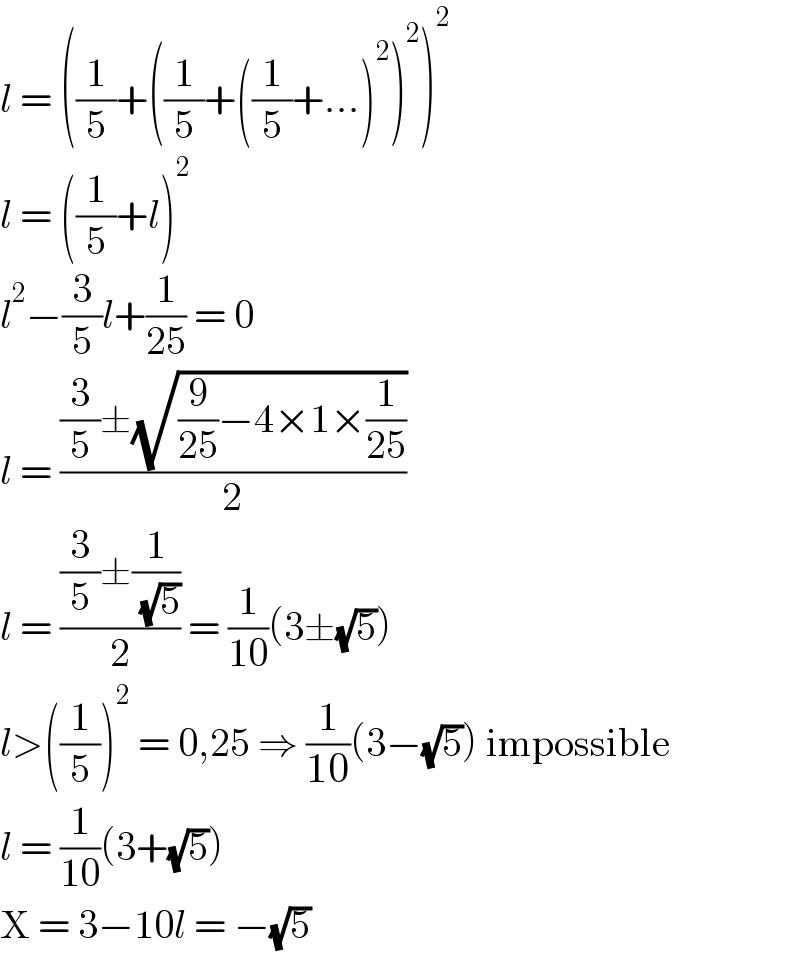
$${l}\:=\:\left(\frac{\mathrm{1}}{\mathrm{5}}+\left(\frac{\mathrm{1}}{\mathrm{5}}+\left(\frac{\mathrm{1}}{\mathrm{5}}+…\right)^{\mathrm{2}} \right)^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${l}\:=\:\left(\frac{\mathrm{1}}{\mathrm{5}}+{l}\right)^{\mathrm{2}} \\ $$$${l}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{5}}{l}+\frac{\mathrm{1}}{\mathrm{25}}\:=\:\mathrm{0} \\ $$$${l}\:=\:\frac{\frac{\mathrm{3}}{\mathrm{5}}\pm\sqrt{\frac{\mathrm{9}}{\mathrm{25}}−\mathrm{4}×\mathrm{1}×\frac{\mathrm{1}}{\mathrm{25}}}}{\mathrm{2}} \\ $$$${l}\:=\:\frac{\frac{\mathrm{3}}{\mathrm{5}}\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{3}\pm\sqrt{\mathrm{5}}\right) \\ $$$${l}>\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} \:=\:\mathrm{0},\mathrm{25}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)\:\mathrm{impossible} \\ $$$${l}\:=\:\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{3}+\sqrt{\mathrm{5}}\right) \\ $$$$\mathrm{X}\:=\:\mathrm{3}−\mathrm{10}{l}\:=\:−\sqrt{\mathrm{5}} \\ $$
