Question-147260

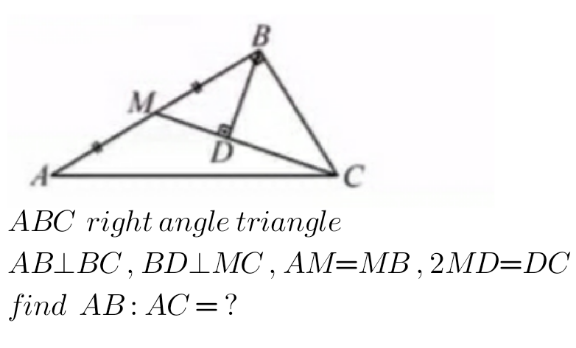
Question Number 147260 by mathdanisur last updated on 19/Jul/21

Answered by Rasheed.Sindhi last updated on 19/Jul/21

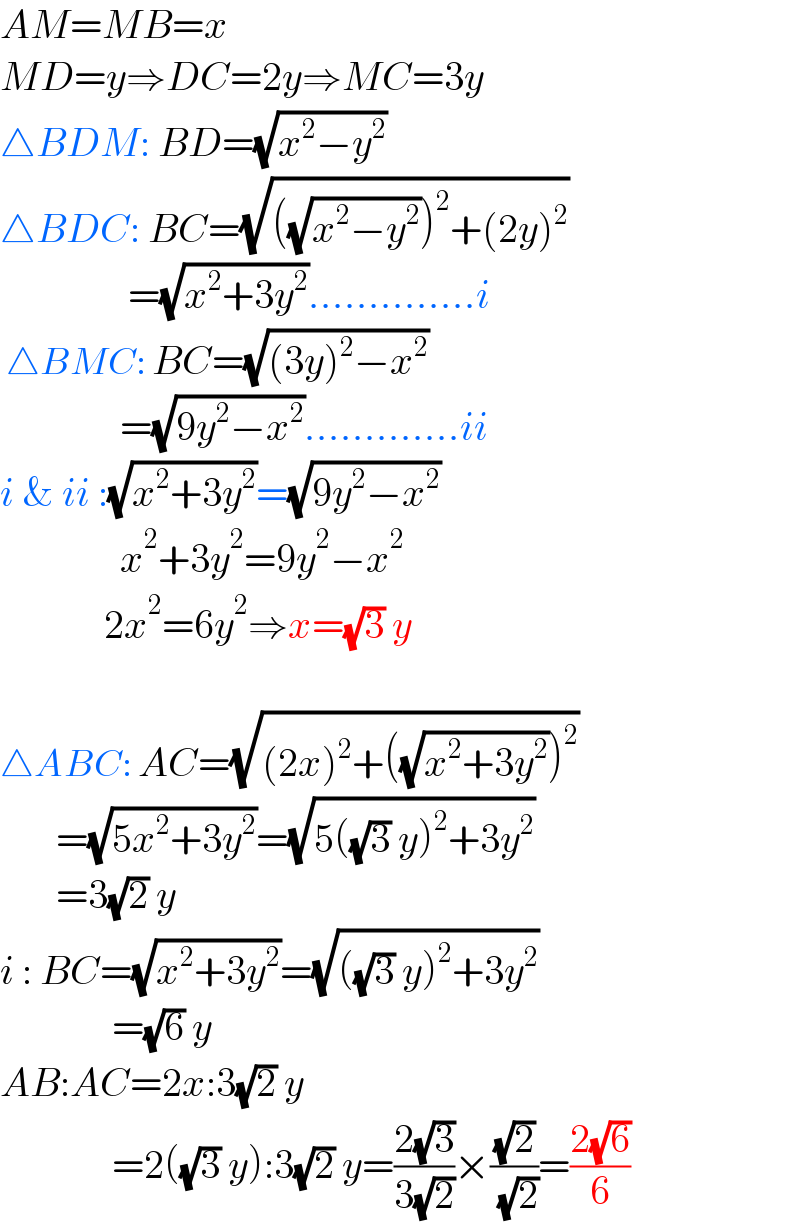
AM=MB=x MD=y⇒DC=2y⇒MC=3y △BDM: BD=(√(x^2 −y^2 )) △BDC: BC=(√(((√(x^2 −y^2 )))^2 +(2y)^2 )) =(√(x^2 +3y^2 ))..............i △BMC: BC=(√((3y)^2 −x^2 )) =(√(9y^2 −x^2 )).............ii i & ii :(√(x^2 +3y^2 ))=(√(9y^2 −x^2 )) x^2 +3y^2 =9y^2 −x^2 2x^2 =6y^2 ⇒x=(√3) y △ABC: AC=(√((2x)^2 +((√(x^2 +3y^2 )))^2 )) =(√(5x^2 +3y^2 ))=(√(5((√3) y)^2 +3y^2 )) =3(√2) y i : BC=(√(x^2 +3y^2 ))=(√(((√3) y)^2 +3y^2 )) =(√6) y AB:AC=2x:3(√2) y =2((√3) y):3(√2) y=((2(√3))/(3(√2)))×((√2)/( (√2)))=((2(√6))/6)

$${AM}={MB}={x} \\ $$$${MD}={y}\Rightarrow{DC}=\mathrm{2}{y}\Rightarrow{MC}=\mathrm{3}{y} \\ $$$$\bigtriangleup{BDM}:\:{BD}=\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$\bigtriangleup{BDC}:\:{BC}=\sqrt{\left(\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\mathrm{2}{y}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }…………..{i} \\ $$$$\:\bigtriangleup{BMC}:\:{BC}=\sqrt{\left(\mathrm{3}{y}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{9}{y}^{\mathrm{2}} −{x}^{\mathrm{2}} }………….{ii} \\ $$$${i}\:\&\:{ii}\::\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }=\sqrt{\mathrm{9}{y}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} =\mathrm{9}{y}^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} =\mathrm{6}{y}^{\mathrm{2}} \Rightarrow{x}=\sqrt{\mathrm{3}}\:{y} \\ $$$$ \\ $$$$\bigtriangleup{ABC}:\:{AC}=\sqrt{\left(\mathrm{2}{x}\right)^{\mathrm{2}} +\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }=\sqrt{\mathrm{5}\left(\sqrt{\mathrm{3}}\:{y}\right)^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\mathrm{3}\sqrt{\mathrm{2}}\:{y} \\ $$$${i}\::\:{BC}=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} }=\sqrt{\left(\sqrt{\mathrm{3}}\:{y}\right)^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{6}}\:{y} \\ $$$${AB}:{AC}=\mathrm{2}{x}:\mathrm{3}\sqrt{\mathrm{2}}\:{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\sqrt{\mathrm{3}}\:{y}\right):\mathrm{3}\sqrt{\mathrm{2}}\:{y}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\mathrm{2}}}×\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{6}} \\ $$

Commented by mathdanisur last updated on 20/Jul/21

$${thank}\:{you}\:{Ser} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply