Question Number 147312 by mathdanisur last updated on 19/Jul/21

Answered by Olaf_Thorendsen last updated on 19/Jul/21
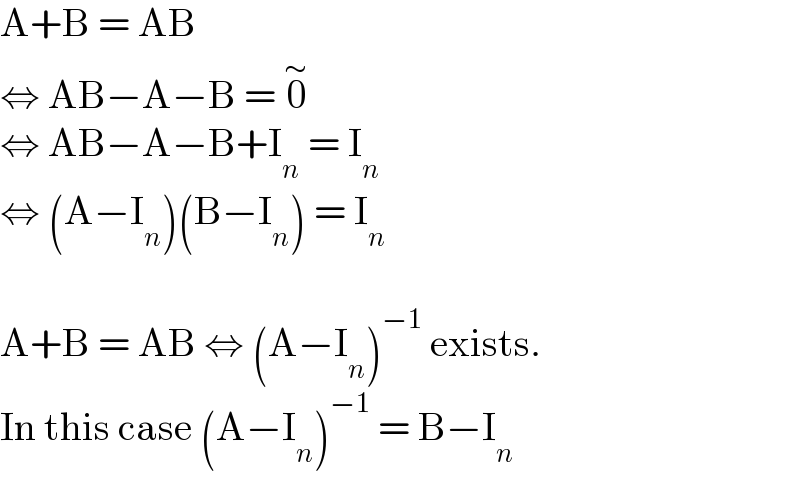
$$\mathrm{A}+\mathrm{B}\:=\:\mathrm{AB} \\ $$$$\Leftrightarrow\:\mathrm{AB}−\mathrm{A}−\mathrm{B}\:=\:\overset{\sim} {\mathrm{0}} \\ $$$$\Leftrightarrow\:\mathrm{AB}−\mathrm{A}−\mathrm{B}+\mathrm{I}_{{n}} \:=\:\mathrm{I}_{{n}} \\ $$$$\Leftrightarrow\:\left(\mathrm{A}−\mathrm{I}_{{n}} \right)\left(\mathrm{B}−\mathrm{I}_{{n}} \right)\:=\:\mathrm{I}_{{n}} \\ $$$$ \\ $$$$\mathrm{A}+\mathrm{B}\:=\:\mathrm{AB}\:\Leftrightarrow\:\left(\mathrm{A}−\mathrm{I}_{{n}} \right)^{−\mathrm{1}} \:\mathrm{exists}. \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case}\:\left(\mathrm{A}−\mathrm{I}_{{n}} \right)^{−\mathrm{1}} \:=\:\mathrm{B}−\mathrm{I}_{{n}} \\ $$
Commented by mathdanisur last updated on 20/Jul/21
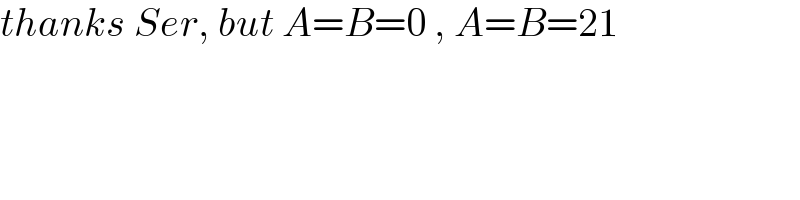
$${thanks}\:{Ser},\:{but}\:{A}={B}=\mathrm{0}\:,\:{A}={B}=\mathrm{21} \\ $$
Commented by mathdanisur last updated on 20/Jul/21
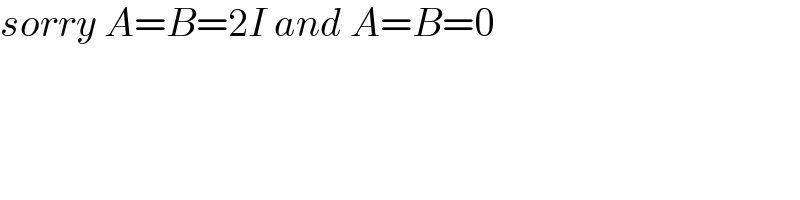
$${sorry}\:{A}={B}=\mathrm{2}{I}\:{and}\:{A}={B}=\mathrm{0} \\ $$
