Question-147411

Question Number 147411 by mnjuly1970 last updated on 20/Jul/21

Answered by mnjuly1970 last updated on 20/Jul/21

:=^((√x) := y) ∫_0 ^( ∞) ((2y dy)/(1+e^( y) )) =2 ∫_0 ^( ∞) ((ydy)/(1+e^( y) )) := 2 η (2) Γ (2)=2.(π^( 2) /(12)) = (π^( 2) /6)

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\::\overset{\sqrt{{x}}\::=\:{y}} {=}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2}{y}\:{dy}}{\mathrm{1}+{e}^{\:{y}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\:\infty} \frac{{ydy}}{\mathrm{1}+{e}^{\:{y}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\::=\:\mathrm{2}\:\eta\:\left(\mathrm{2}\right)\:\Gamma\:\left(\mathrm{2}\right)=\mathrm{2}.\frac{\pi^{\:\mathrm{2}} }{\mathrm{12}}\:=\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by tabata last updated on 20/Jul/21

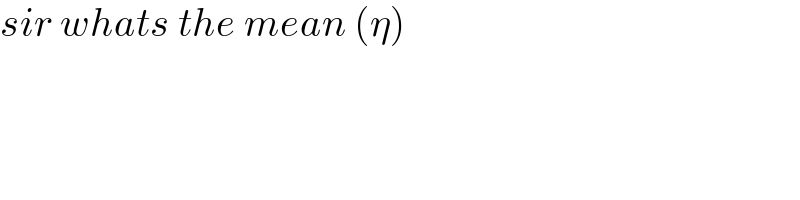
$${sir}\:{whats}\:{the}\:{mean}\:\left(\eta\right) \\ $$

Commented by mnjuly1970 last updated on 20/Jul/21

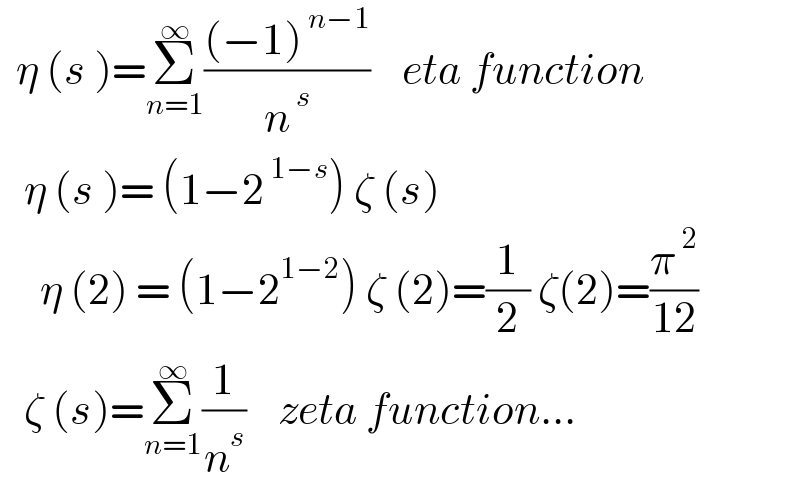
η (s )=Σ_(n=1) ^∞ (((−1)^( n−1) )/n^( s) ) eta function η (s )= (1−2^( 1−s) ) ζ (s) η (2) = (1−2^(1−2) ) ζ (2)=(1/2) ζ(2)=(π^( 2) /(12)) ζ (s)=Σ_(n=1) ^∞ (1/n^s ) zeta function...

$$\:\:\eta\:\left({s}\:\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} }{{n}^{\:{s}} }\:\:\:\:{eta}\:{function} \\ $$$$\:\:\:\eta\:\left({s}\:\right)=\:\left(\mathrm{1}−\mathrm{2}^{\:\mathrm{1}−{s}} \right)\:\zeta\:\left({s}\right) \\ $$$$\:\:\:\:\:\eta\:\left(\mathrm{2}\right)\:=\:\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\mathrm{2}} \right)\:\zeta\:\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\zeta\left(\mathrm{2}\right)=\frac{\pi^{\:\mathrm{2}} }{\mathrm{12}}\: \\ $$$$\:\:\:\zeta\:\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} }\:\:\:\:{zeta}\:{function}… \\ $$

Commented by Olaf_Thorendsen last updated on 20/Jul/21

$$\mathrm{the}\:\mathrm{Dirichlet}\:\mathrm{eta}\:\mathrm{function} \\ $$

Answered by Olaf_Thorendsen last updated on 20/Jul/21

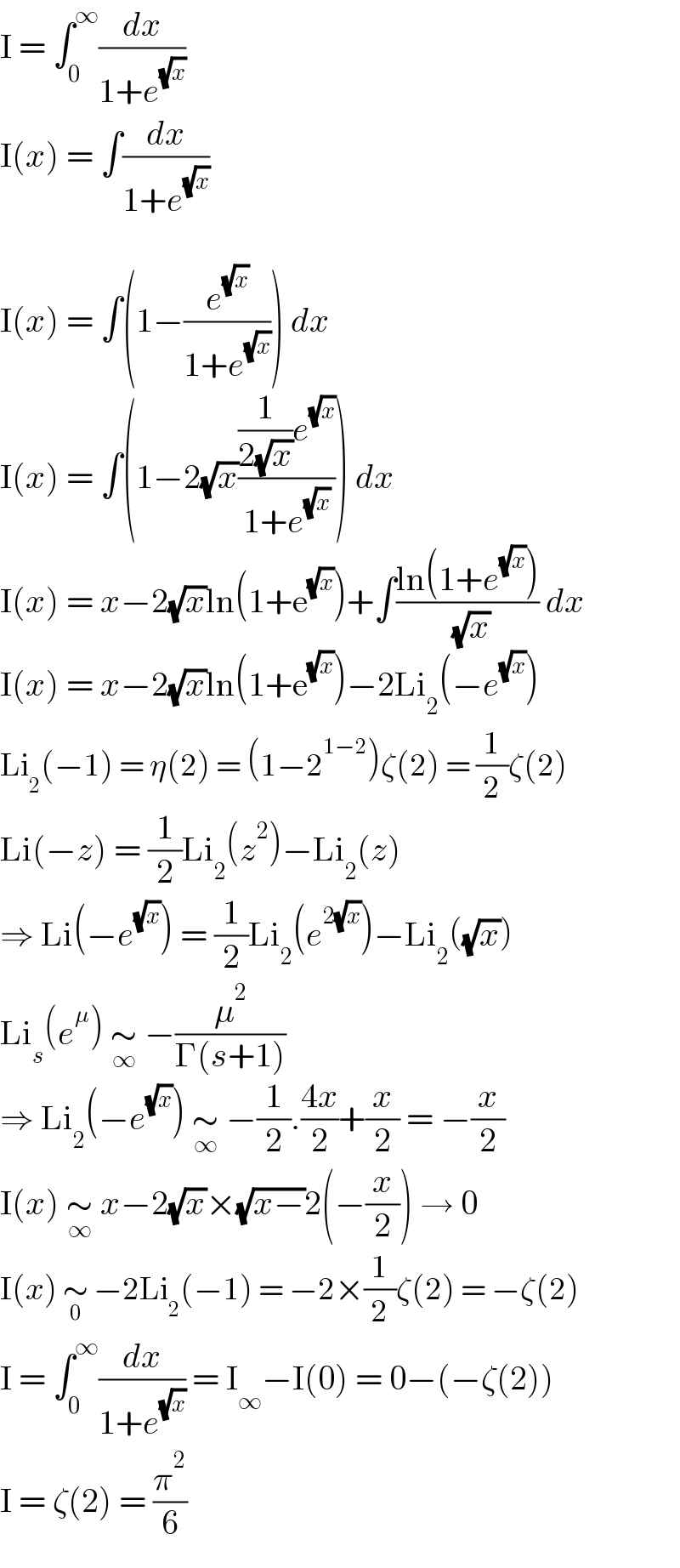
I = ∫_0 ^∞ (dx/(1+e^(√x) )) I(x) = ∫(dx/(1+e^(√x) )) I(x) = ∫(1−(e^(√x) /(1+e^(√x) ))) dx I(x) = ∫(1−2(√x)(((1/(2(√x)))e^(√x) )/(1+e^(√x) ))) dx I(x) = x−2(√x)ln(1+e^(√x) )+∫((ln(1+e^(√x) ))/( (√x))) dx I(x) = x−2(√x)ln(1+e^(√x) )−2Li_2 (−e^(√x) ) Li_2 (−1) = η(2) = (1−2^(1−2) )ζ(2) = (1/2)ζ(2) Li(−z) = (1/2)Li_2 (z^2 )−Li_2 (z) ⇒ Li(−e^(√x) ) = (1/2)Li_2 (e^(2(√x)) )−Li_2 ((√x)) Li_s (e^μ ) ∼_∞ −(μ^2 /(Γ(s+1))) ⇒ Li_2 (−e^(√x) ) ∼_∞ −(1/2).((4x)/2)+(x/2) = −(x/2) I(x) ∼_∞ x−2(√x)×(√(x−))2(−(x/2)) → 0 I(x) ∼_0 −2Li_2 (−1) = −2×(1/2)ζ(2) = −ζ(2) I = ∫_0 ^∞ (dx/(1+e^(√x) )) = I_∞ −I(0) = 0−(−ζ(2)) I = ζ(2) = (π^2 /6)

$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{e}^{\sqrt{{x}}} } \\ $$$$\mathrm{I}\left({x}\right)\:=\:\int\frac{{dx}}{\mathrm{1}+{e}^{\sqrt{{x}}} } \\ $$$$ \\ $$$$\mathrm{I}\left({x}\right)\:=\:\int\left(\mathrm{1}−\frac{{e}^{\sqrt{{x}}} }{\mathrm{1}+{e}^{\sqrt{{x}}} }\right)\:{dx} \\ $$$$\mathrm{I}\left({x}\right)\:=\:\int\left(\mathrm{1}−\mathrm{2}\sqrt{{x}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{e}^{\sqrt{{x}}} }{\mathrm{1}+{e}^{\sqrt{{x}}} }\right)\:{dx} \\ $$$$\mathrm{I}\left({x}\right)\:=\:{x}−\mathrm{2}\sqrt{{x}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\sqrt{{x}}} \right)+\int\frac{\mathrm{ln}\left(\mathrm{1}+{e}^{\sqrt{{x}}} \right)}{\:\sqrt{{x}}}\:{dx} \\ $$$$\mathrm{I}\left({x}\right)\:=\:{x}−\mathrm{2}\sqrt{{x}}\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\sqrt{{x}}} \right)−\mathrm{2Li}_{\mathrm{2}} \left(−{e}^{\sqrt{{x}}} \right) \\ $$$$\mathrm{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)\:=\:\eta\left(\mathrm{2}\right)\:=\:\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\mathrm{2}} \right)\zeta\left(\mathrm{2}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right) \\ $$$$\mathrm{Li}\left(−{z}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \left({z}^{\mathrm{2}} \right)−\mathrm{Li}_{\mathrm{2}} \left({z}\right) \\ $$$$\Rightarrow\:\mathrm{Li}\left(−{e}^{\sqrt{{x}}} \right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \left({e}^{\mathrm{2}\sqrt{{x}}} \right)−\mathrm{Li}_{\mathrm{2}} \left(\sqrt{{x}}\right) \\ $$$$\mathrm{Li}_{{s}} \left({e}^{\mu} \right)\:\underset{\infty} {\sim}\:−\frac{\mu^{\mathrm{2}} }{\Gamma\left({s}+\mathrm{1}\right)} \\ $$$$\Rightarrow\:\mathrm{Li}_{\mathrm{2}} \left(−{e}^{\sqrt{{x}}} \right)\:\underset{\infty} {\sim}\:−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{4}{x}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}}\:=\:−\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{I}\left({x}\right)\:\underset{\infty} {\sim}\:{x}−\mathrm{2}\sqrt{{x}}×\sqrt{{x}−}\mathrm{2}\left(−\frac{{x}}{\mathrm{2}}\right)\:\rightarrow\:\mathrm{0} \\ $$$$\mathrm{I}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:−\mathrm{2Li}_{\mathrm{2}} \left(−\mathrm{1}\right)\:=\:−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)\:=\:−\zeta\left(\mathrm{2}\right) \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{e}^{\sqrt{{x}}} }\:=\:\mathrm{I}_{\infty} −\mathrm{I}\left(\mathrm{0}\right)\:=\:\mathrm{0}−\left(−\zeta\left(\mathrm{2}\right)\right) \\ $$$$\mathrm{I}\:=\:\zeta\left(\mathrm{2}\right)\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by Tawa11 last updated on 03/Aug/21

$$\mathrm{Great} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply