Question-147474

Question Number 147474 by mnjuly1970 last updated on 21/Jul/21

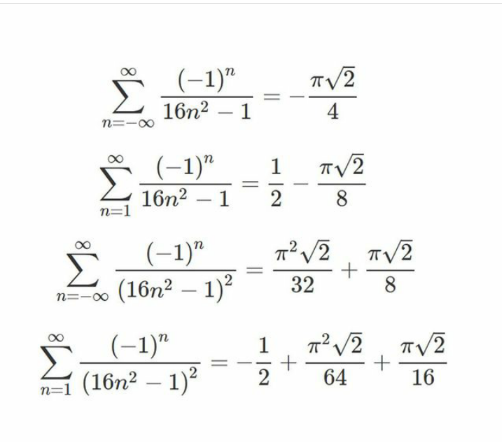
Answered by mindispower last updated on 21/Jul/21

(1/(2a))(Σ_(n≥−∞) ^∞ (((−1)^n )/(4n−a))−(((−1)^n )/(4n+a)))=Σ_(n≥−∞) (((−1)^n )/(16n^2 −a^2 ))=f(a) =(1/(2a))Σ_(n≥−∞) (1/(8n−a))−(1/(8n−a+4))−(1/(8n+a))+(1/(8n+a+4)) recall Σ_(n≥−∞) (1/(x+n))=πcot(πx) f(a)=(π/(16a))(cot(−((πa)/8))−cot(((4−a)/8)π)−cot(((πa)/8))+cot(((4+a)/8)π)) =−(π/(8a))(cot(((πa)/8))+tan(((πa)/8))) cot(a)+tan(a)=(2/(sin(2a))) =−(π/(4asin(((πa)/4)))) (1)=f(1)=(π/(4sin((π/4))))=−(π/4)(√2) (2) f(1)=2S−1⇒s=(1/2)−(π/(4(√2))) (3)f′(a)=Σ_(n≥−∞) ((2a(−1)^n )/((16n^2 −a^2 )^2 )) S=((f′(1))/2) f′(a)=(π/4)(((sin(((πa)/4))+(π/4)acos((π/4)a))/((asin((π/4)a))^2 ))) f′(1)=(π/4)((√2)+(π/4)(√2))=(π^2 /(16))(√2)+((π(√2))/4) S=(π^2 /(32))(√2)+((π(√2))/8) (4),S=2S′+1 S′=(π^2 /(64))(√2)+((π(√2))/(16))−(1/2)

$$\frac{\mathrm{1}}{\mathrm{2}{a}}\left(\underset{{n}\geqslant−\infty} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}−{a}}−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+{a}}\right)=\underset{{n}\geqslant−\infty} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{16}{n}^{\mathrm{2}} −{a}^{\mathrm{2}} }={f}\left({a}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}\underset{{n}\geqslant−\infty} {\sum}\frac{\mathrm{1}}{\mathrm{8}{n}−{a}}−\frac{\mathrm{1}}{\mathrm{8}{n}−{a}+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}{n}+{a}}+\frac{\mathrm{1}}{\mathrm{8}{n}+{a}+\mathrm{4}} \\ $$$${recall}\:\underset{{n}\geqslant−\infty} {\sum}\frac{\mathrm{1}}{{x}+{n}}=\pi{cot}\left(\pi{x}\right) \\ $$$${f}\left({a}\right)=\frac{\pi}{\mathrm{16}{a}}\left({cot}\left(−\frac{\pi{a}}{\mathrm{8}}\right)−{cot}\left(\frac{\mathrm{4}−{a}}{\mathrm{8}}\pi\right)−{cot}\left(\frac{\pi{a}}{\mathrm{8}}\right)+{cot}\left(\frac{\mathrm{4}+{a}}{\mathrm{8}}\pi\right)\right) \\ $$$$=−\frac{\pi}{\mathrm{8}{a}}\left({cot}\left(\frac{\pi{a}}{\mathrm{8}}\right)+{tan}\left(\frac{\pi{a}}{\mathrm{8}}\right)\right) \\ $$$${cot}\left({a}\right)+{tan}\left({a}\right)=\frac{\mathrm{2}}{{sin}\left(\mathrm{2}{a}\right)} \\ $$$$=−\frac{\pi}{\mathrm{4}{asin}\left(\frac{\pi{a}}{\mathrm{4}}\right)} \\ $$$$\left(\mathrm{1}\right)={f}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=−\frac{\pi}{\mathrm{4}}\sqrt{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:{f}\left(\mathrm{1}\right)=\mathrm{2}{S}−\mathrm{1}\Rightarrow{s}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$\left(\mathrm{3}\right){f}'\left({a}\right)=\underset{{n}\geqslant−\infty} {\sum}\frac{\mathrm{2}{a}\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{16}{n}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${S}=\frac{{f}'\left(\mathrm{1}\right)}{\mathrm{2}} \\ $$$${f}'\left({a}\right)=\frac{\pi}{\mathrm{4}}\left(\frac{{sin}\left(\frac{\pi{a}}{\mathrm{4}}\right)+\frac{\pi}{\mathrm{4}}{acos}\left(\frac{\pi}{\mathrm{4}}{a}\right)}{\left({asin}\left(\frac{\pi}{\mathrm{4}}{a}\right)\right)^{\mathrm{2}} }\right) \\ $$$${f}'\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}}\left(\sqrt{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\sqrt{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\sqrt{\mathrm{2}}+\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${S}=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}\sqrt{\mathrm{2}}+\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\left(\mathrm{4}\right),{S}=\mathrm{2}{S}'+\mathrm{1} \\ $$$${S}'=\frac{\pi^{\mathrm{2}} }{\mathrm{64}}\sqrt{\mathrm{2}}+\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply