Question Number 147477 by vvvv last updated on 21/Jul/21
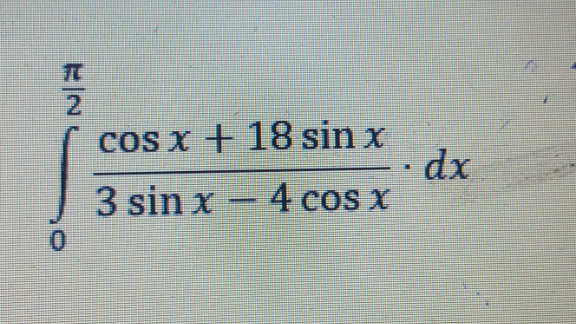
Commented by Rustambek last updated on 21/Jul/21

$${salom} \\ $$
Answered by puissant last updated on 21/Jul/21
![=∫_0 ^( (π/2)) ((cos(x)+18sin(x))/(−4cos(x)+3sin(x))) dx =[(((1×(−4)+3×18)/((−4)^2 +3^3 )))x + (((1×3−18×(−4))/((−4)^2 +3^2 )))ln∣−4cos(x)+3sin(x)∣]_0 ^(π/2) =[2x+3ln∣−4cos(x)+3sin(x)∣]_0 ^(π/2) =(π+3ln3)−3ln4 ⇒I= π+3ln((3/4))...](https://www.tinkutara.com/question/Q147480.png)
$$=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{cos}\left({x}\right)+\mathrm{18}{sin}\left({x}\right)}{−\mathrm{4}{cos}\left({x}\right)+\mathrm{3}{sin}\left({x}\right)}\:{dx} \\ $$$$=\left[\left(\frac{\mathrm{1}×\left(−\mathrm{4}\right)+\mathrm{3}×\mathrm{18}}{\left(−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} }\right){x}\:+\:\left(\frac{\mathrm{1}×\mathrm{3}−\mathrm{18}×\left(−\mathrm{4}\right)}{\left(−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }\right){ln}\mid−\mathrm{4}{cos}\left({x}\right)+\mathrm{3}{sin}\left({x}\right)\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\left[\mathrm{2}{x}+\mathrm{3}{ln}\mid−\mathrm{4}{cos}\left({x}\right)+\mathrm{3}{sin}\left({x}\right)\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\left(\pi+\mathrm{3}{ln}\mathrm{3}\right)−\mathrm{3}{ln}\mathrm{4} \\ $$$$\Rightarrow{I}=\:\pi+\mathrm{3}{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)… \\ $$
Commented by vvvv last updated on 21/Jul/21

$$\boldsymbol{{yes}}\:\:\boldsymbol{{prove}}\:\boldsymbol{{is}}\:\boldsymbol{{formulas}} \\ $$
Commented by gsk2684 last updated on 21/Jul/21
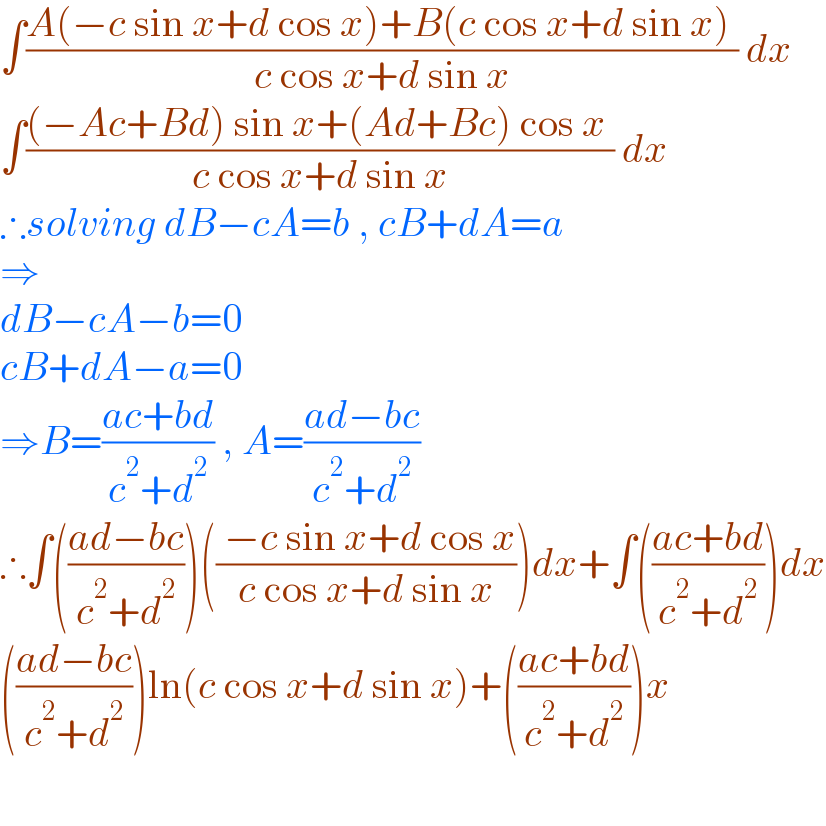
$$\int\frac{{A}\left(−{c}\:\mathrm{sin}\:{x}+{d}\:\mathrm{cos}\:{x}\right)+{B}\left({c}\:\mathrm{cos}\:{x}+{d}\:\mathrm{sin}\:{x}\right)\:}{{c}\:\mathrm{cos}\:{x}+{d}\:\mathrm{sin}\:{x}}\:{dx} \\ $$$$\int\frac{\left(−{Ac}+{Bd}\right)\:\mathrm{sin}\:{x}+\left({Ad}+{Bc}\right)\:\mathrm{cos}\:{x}\:}{{c}\:\mathrm{cos}\:{x}+{d}\:\mathrm{sin}\:{x}}\:{dx} \\ $$$$\therefore{solving}\:{dB}−{cA}={b}\:,\:{cB}+{dA}={a} \\ $$$$\Rightarrow \\ $$$${dB}−{cA}−{b}=\mathrm{0} \\ $$$${cB}+{dA}−{a}=\mathrm{0} \\ $$$$\Rightarrow{B}=\frac{{ac}+{bd}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\:,\:{A}=\frac{{ad}−{bc}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$$\therefore\int\left(\frac{{ad}−{bc}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right)\left(\frac{\:−{c}\:\mathrm{sin}\:{x}+{d}\:\mathrm{cos}\:{x}}{{c}\:\mathrm{cos}\:{x}+{d}\:\mathrm{sin}\:{x}}\right){dx}+\int\left(\frac{{ac}+{bd}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right){dx} \\ $$$$\left(\frac{{ad}−{bc}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right)\mathrm{ln}\left({c}\:\mathrm{cos}\:{x}+{d}\:\mathrm{sin}\:{x}\right)+\left(\frac{{ac}+{bd}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right){x} \\ $$$$ \\ $$
Commented by vvvv last updated on 21/Jul/21

$$? \\ $$
Commented by puissant last updated on 21/Jul/21
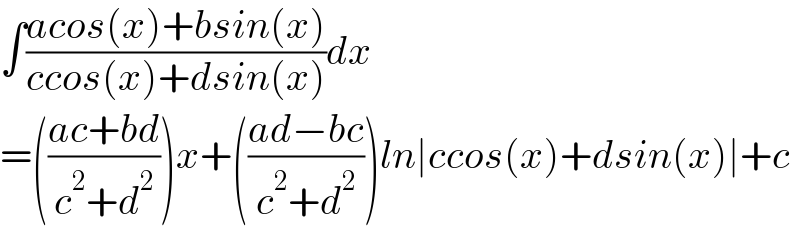
$$\int\frac{{acos}\left({x}\right)+{bsin}\left({x}\right)}{{ccos}\left({x}\right)+{dsin}\left({x}\right)}{dx} \\ $$$$=\left(\frac{{ac}+{bd}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right){x}+\left(\frac{{ad}−{bc}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\right){ln}\mid{ccos}\left({x}\right)+{dsin}\left({x}\right)\mid+{c} \\ $$
Commented by mathmax by abdo last updated on 21/Jul/21
![I=∫_0 ^(π/2) ((cosx+18sinx)/(4cosx−3sinx))dx ⇒I=∫_0 ^(π/2) ((1+18tanx)/(4−3tanx))dx =_(tanx=t) ∫_0 ^∞ ((1+18t)/(4−3t))×(dt/(1+t^2 )) =−∫_0 ^∞ ((18t+1)/((3t−4)(t^2 +1)))dt let decompose F(t)=((18t+1)/((3t−4)(t^2 +1))) F(t)=(a/(3t−4))+((bt+c)/(t^2 +1)) a=((18.(4/3)+1)/(((16)/9)+1))=((25)/(25))×9 =9 lim_(t→∞) tF(t)=0=(a/3)+b ⇒b=−(9/3)=−3 F(0)=−(1/4)=−(a/4)+c =−(9/4)+c ⇒c=(9/4)−(1/4)=2 ⇒ F(t)=(9/(3t−4))+((−3t+2)/(t^2 +1)) ⇒ ∫_0 ^∞ F(t)dt =3∫_0 ^∞ ((1/(t−(4/3)))−(3/2)×((2t)/(t^2 +1)) +(2/(t^2 +1)))dt =3[log∣((t−(4/3))/( (√(t^2 +1))))∣]_0 ^∞ +6[arctant]_0 ^∞ =3(−log((4/3)))+6((π/2))=3π−3log((4/3)) ⇒ I=3log((4/3))−3π =6log2−3log3−3π](https://www.tinkutara.com/question/Q147491.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{cosx}+\mathrm{18sinx}}{\mathrm{4cosx}−\mathrm{3sinx}}\mathrm{dx}\:\Rightarrow\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{18tanx}}{\mathrm{4}−\mathrm{3tanx}}\mathrm{dx} \\ $$$$=_{\mathrm{tanx}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\mathrm{18t}}{\mathrm{4}−\mathrm{3t}}×\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{18t}+\mathrm{1}}{\left(\mathrm{3t}−\mathrm{4}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{18t}+\mathrm{1}}{\left(\mathrm{3t}−\mathrm{4}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}}{\mathrm{3t}−\mathrm{4}}+\frac{\mathrm{bt}+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{a}=\frac{\mathrm{18}.\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{1}}{\frac{\mathrm{16}}{\mathrm{9}}+\mathrm{1}}=\frac{\mathrm{25}}{\mathrm{25}}×\mathrm{9}\:=\mathrm{9} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow\infty} \mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}=\frac{\mathrm{a}}{\mathrm{3}}+\mathrm{b}\:\Rightarrow\mathrm{b}=−\frac{\mathrm{9}}{\mathrm{3}}=−\mathrm{3} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)=−\frac{\mathrm{1}}{\mathrm{4}}=−\frac{\mathrm{a}}{\mathrm{4}}+\mathrm{c}\:=−\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{c}\:\Rightarrow\mathrm{c}=\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{9}}{\mathrm{3t}−\mathrm{4}}+\frac{−\mathrm{3t}+\mathrm{2}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{3}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{t}−\frac{\mathrm{4}}{\mathrm{3}}}−\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\:+\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{dt} \\ $$$$=\mathrm{3}\left[\mathrm{log}\mid\frac{\mathrm{t}−\frac{\mathrm{4}}{\mathrm{3}}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}}\mid\right]_{\mathrm{0}} ^{\infty} +\mathrm{6}\left[\mathrm{arctant}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\mathrm{3}\left(−\mathrm{log}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\right)+\mathrm{6}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{3}\pi−\mathrm{3log}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:\Rightarrow \\ $$$$\mathrm{I}=\mathrm{3log}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)−\mathrm{3}\pi\:=\mathrm{6log2}−\mathrm{3log3}−\mathrm{3}\pi \\ $$
