Question Number 147507 by puissant last updated on 21/Jul/21

Commented by Olaf_Thorendsen last updated on 21/Jul/21

$$\mathrm{Les}\:\mathrm{donnees}\:\mathrm{numeriques}\:\mathrm{semblent} \\ $$$$\mathrm{tres}\:\mathrm{curieuses}. \\ $$
Commented by puissant last updated on 21/Jul/21
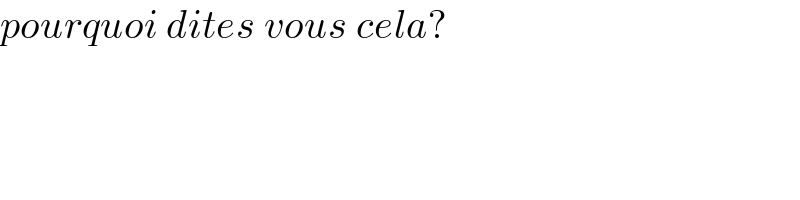
$${pourquoi}\:{dites}\:{vous}\:{cela}? \\ $$
Answered by Olaf_Thorendsen last updated on 21/Jul/21
![M est l′indice pour monsieur Mombo N est l′indice pour madame Nstame 1) • 0 ≤ t≤ 5s : α = 2,5m.s^(−1) v_M (t) = αt = 2,5t [m.s^(−1) ] x_M (t) = ∫v_M (t)dt = (1/2)αt^2 = 1,25t^2 [m] • t = 5s : v_M (5) = 2,5×5 = 12,5m.s^(−1) x_M (5) = 1,25×5^2 = 31,25m • t > 5s : v_M (t) = v_M (5) = 12,5m.s^(−1) x_M (t) = 31,25+12,5(t−5) x_M (t) = 12,5t−31,25 [m] Et donc : x_M (t) = { ((1,25t^2 si 0 ≤ t≤ 5s)),((12,5t−31,25 si t ≥ 5s)) :} v_N (t) = cste = 60 km.h^(−1) v_N (t) = ((60)/(3,6)) = ((50)/3) = 16,7 m.s^(−1) = v_N 1er cas : Si N roule dans le meme sens que M alors : x_N (t) = v_N t−25 = ((50)/3)t−25 2eme cas : Si N roule dans le sens oppose a celui de M alors : x_N (t) = 25−v_N t = 25−((50)/3)t 2) 1er cas : meme sens si t = 5s, x_N (5) = ((50)/3)5−25 ≈ 58,3m et x_M (5) = 31,25m x_N >x_M donc N a eu le temps de depasser M dans les 5 premieres secondes. Quand ? Quand 1,25t^2 = ((50)/3)t−25 ⇒ t ≈ 1,72s 2eme cas : sens oppose Meme raisonnement et ici Quand 1,25t^2 = 25−((50)/3)t ⇒ t ≈ 1,36s 3) Lors des croisements x_M = x_N = 1er cas : 1,25×1,72^2 = 3,70m 2eme cas : 1,25×1,36 = 2,31m La vitesse de M est alors : 1er cas : 2,5×1,72 = 4,3 m.s^(−1) 2eme cas : 2,5×1,36 = 3,4 m.s^(−1)](https://www.tinkutara.com/question/Q147521.png)
$$\mathrm{M}\:\mathrm{est}\:\mathrm{l}'\mathrm{indice}\:\mathrm{pour}\:\mathrm{monsieur}\:\mathrm{Mombo} \\ $$$$\mathrm{N}\:\mathrm{est}\:\mathrm{l}'\mathrm{indice}\:\mathrm{pour}\:\mathrm{madame}\:\mathrm{Nstame} \\ $$$$ \\ $$$$\left.\mathrm{1}\right) \\ $$$$ \\ $$$$\bullet\:\mathrm{0}\:\leqslant\:{t}\leqslant\:\mathrm{5}{s}\:: \\ $$$$\alpha\:=\:\mathrm{2},\mathrm{5}{m}.{s}^{−\mathrm{1}} \\ $$$${v}_{\mathrm{M}} \left({t}\right)\:=\:\alpha{t}\:=\:\mathrm{2},\mathrm{5}{t}\:\left[{m}.{s}^{−\mathrm{1}} \right] \\ $$$${x}_{\mathrm{M}} \left({t}\right)\:=\:\int{v}_{\mathrm{M}} \left({t}\right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\alpha{t}^{\mathrm{2}} \:=\:\mathrm{1},\mathrm{25}{t}^{\mathrm{2}} \:\left[{m}\right] \\ $$$$ \\ $$$$\bullet\:{t}\:=\:\mathrm{5}{s}\::\:{v}_{\mathrm{M}} \left(\mathrm{5}\right)\:=\:\mathrm{2},\mathrm{5}×\mathrm{5}\:=\:\mathrm{12},\mathrm{5}{m}.{s}^{−\mathrm{1}} \\ $$$${x}_{\mathrm{M}} \left(\mathrm{5}\right)\:=\:\mathrm{1},\mathrm{25}×\mathrm{5}^{\mathrm{2}} \:=\:\mathrm{31},\mathrm{25}{m} \\ $$$$ \\ $$$$\bullet\:{t}\:>\:\mathrm{5}{s}\:\::\:{v}_{\mathrm{M}} \left({t}\right)\:=\:{v}_{\mathrm{M}} \left(\mathrm{5}\right)\:=\:\mathrm{12},\mathrm{5}{m}.{s}^{−\mathrm{1}} \\ $$$${x}_{\mathrm{M}} \left({t}\right)\:=\:\mathrm{31},\mathrm{25}+\mathrm{12},\mathrm{5}\left({t}−\mathrm{5}\right) \\ $$$${x}_{\mathrm{M}} \left({t}\right)\:=\:\mathrm{12},\mathrm{5}{t}−\mathrm{31},\mathrm{25}\:\left[{m}\right] \\ $$$$ \\ $$$$\mathrm{Et}\:\mathrm{donc}\:: \\ $$$${x}_{\mathrm{M}} \left({t}\right)\:=\:\begin{cases}{\mathrm{1},\mathrm{25}{t}^{\mathrm{2}} \:\mathrm{si}\:\mathrm{0}\:\leqslant\:{t}\leqslant\:\mathrm{5}{s}}\\{\mathrm{12},\mathrm{5}{t}−\mathrm{31},\mathrm{25}\:\mathrm{si}\:{t}\:\geqslant\:\mathrm{5}{s}}\end{cases} \\ $$$$ \\ $$$${v}_{\mathrm{N}} \left({t}\right)\:=\:\mathrm{cste}\:=\:\mathrm{60}\:{km}.{h}^{−\mathrm{1}} \: \\ $$$${v}_{\mathrm{N}} \left({t}\right)\:=\:\frac{\mathrm{60}}{\mathrm{3},\mathrm{6}}\:=\:\frac{\mathrm{50}}{\mathrm{3}}\:=\:\mathrm{16},\mathrm{7}\:{m}.{s}^{−\mathrm{1}} \:=\:{v}_{\mathrm{N}} \\ $$$$\mathrm{1er}\:\mathrm{cas}\::\:\mathrm{Si}\:\mathrm{N}\:\mathrm{roule}\:\mathrm{dans}\:\mathrm{le}\:\mathrm{meme}\:\mathrm{sens} \\ $$$$\mathrm{que}\:\mathrm{M}\:\mathrm{alors}\:: \\ $$$${x}_{\mathrm{N}} \left({t}\right)\:=\:{v}_{\mathrm{N}} {t}−\mathrm{25}\:=\:\frac{\mathrm{50}}{\mathrm{3}}{t}−\mathrm{25} \\ $$$$\mathrm{2eme}\:\mathrm{cas}\::\:\mathrm{Si}\:\mathrm{N}\:\mathrm{roule}\:\mathrm{dans}\:\mathrm{le}\:\mathrm{sens} \\ $$$$\mathrm{oppose}\:\mathrm{a}\:\mathrm{celui}\:\mathrm{de}\:\mathrm{M}\:\mathrm{alors}\:: \\ $$$${x}_{\mathrm{N}} \left({t}\right)\:=\:\mathrm{25}−{v}_{\mathrm{N}} {t}\:=\:\mathrm{25}−\frac{\mathrm{50}}{\mathrm{3}}{t} \\ $$$$ \\ $$$$\left.\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{1er}\:\mathrm{cas}\::\:\mathrm{meme}\:\mathrm{sens} \\ $$$$\mathrm{si}\:{t}\:=\:\mathrm{5}{s},\:{x}_{\mathrm{N}} \left(\mathrm{5}\right)\:=\:\frac{\mathrm{50}}{\mathrm{3}}\mathrm{5}−\mathrm{25}\:\approx\:\mathrm{58},\mathrm{3}{m} \\ $$$$\mathrm{et}\:{x}_{\mathrm{M}} \left(\mathrm{5}\right)\:=\:\mathrm{31},\mathrm{25}{m} \\ $$$${x}_{\mathrm{N}} >{x}_{\mathrm{M}} \:\mathrm{donc}\:\mathrm{N}\:\mathrm{a}\:\mathrm{eu}\:\mathrm{le}\:\mathrm{temps}\:\mathrm{de} \\ $$$$\mathrm{depasser}\:\mathrm{M}\:\mathrm{dans}\:\mathrm{les}\:\mathrm{5}\:\mathrm{premieres} \\ $$$$\mathrm{secondes}.\:\mathrm{Quand}\:? \\ $$$$\mathrm{Quand}\:\mathrm{1},\mathrm{25}{t}^{\mathrm{2}} \:=\:\frac{\mathrm{50}}{\mathrm{3}}{t}−\mathrm{25}\:\Rightarrow\:{t}\:\approx\:\mathrm{1},\mathrm{72}{s} \\ $$$$ \\ $$$$\mathrm{2eme}\:\mathrm{cas}\::\:\mathrm{sens}\:\mathrm{oppose} \\ $$$$\mathrm{Meme}\:\mathrm{raisonnement}\:\mathrm{et}\:\mathrm{ici} \\ $$$$\mathrm{Quand}\:\mathrm{1},\mathrm{25}{t}^{\mathrm{2}} \:=\:\mathrm{25}−\frac{\mathrm{50}}{\mathrm{3}}{t}\:\Rightarrow\:{t}\:\approx\:\mathrm{1},\mathrm{36}{s} \\ $$$$ \\ $$$$\left.\mathrm{3}\right) \\ $$$$\mathrm{Lors}\:\mathrm{des}\:\mathrm{croisements}\:{x}_{\mathrm{M}} \:=\:{x}_{\mathrm{N}} \:=\: \\ $$$$\mathrm{1er}\:\mathrm{cas}\::\:\mathrm{1},\mathrm{25}×\mathrm{1},\mathrm{72}^{\mathrm{2}} \:=\:\mathrm{3},\mathrm{70}{m} \\ $$$$\mathrm{2eme}\:\mathrm{cas}\::\:\mathrm{1},\mathrm{25}×\mathrm{1},\mathrm{36}\:=\:\mathrm{2},\mathrm{31}{m} \\ $$$$ \\ $$$$\mathrm{La}\:\mathrm{vitesse}\:\mathrm{de}\:\mathrm{M}\:\mathrm{est}\:\mathrm{alors}\:: \\ $$$$\mathrm{1er}\:\mathrm{cas}\::\:\mathrm{2},\mathrm{5}×\mathrm{1},\mathrm{72}\:=\:\mathrm{4},\mathrm{3}\:{m}.{s}^{−\mathrm{1}} \\ $$$$\mathrm{2eme}\:\mathrm{cas}\::\:\mathrm{2},\mathrm{5}×\mathrm{1},\mathrm{36}\:=\:\mathrm{3},\mathrm{4}\:{m}.{s}^{−\mathrm{1}} \\ $$
Commented by puissant last updated on 21/Jul/21

$${merci}\:{prof} \\ $$
