Question-147535

Question Number 147535 by tabata last updated on 21/Jul/21

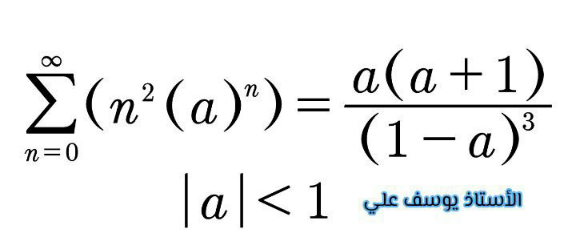
Commented by tabata last updated on 21/Jul/21

$${prove}\:{that} \\ $$

Answered by mathmax by abdo last updated on 21/Jul/21

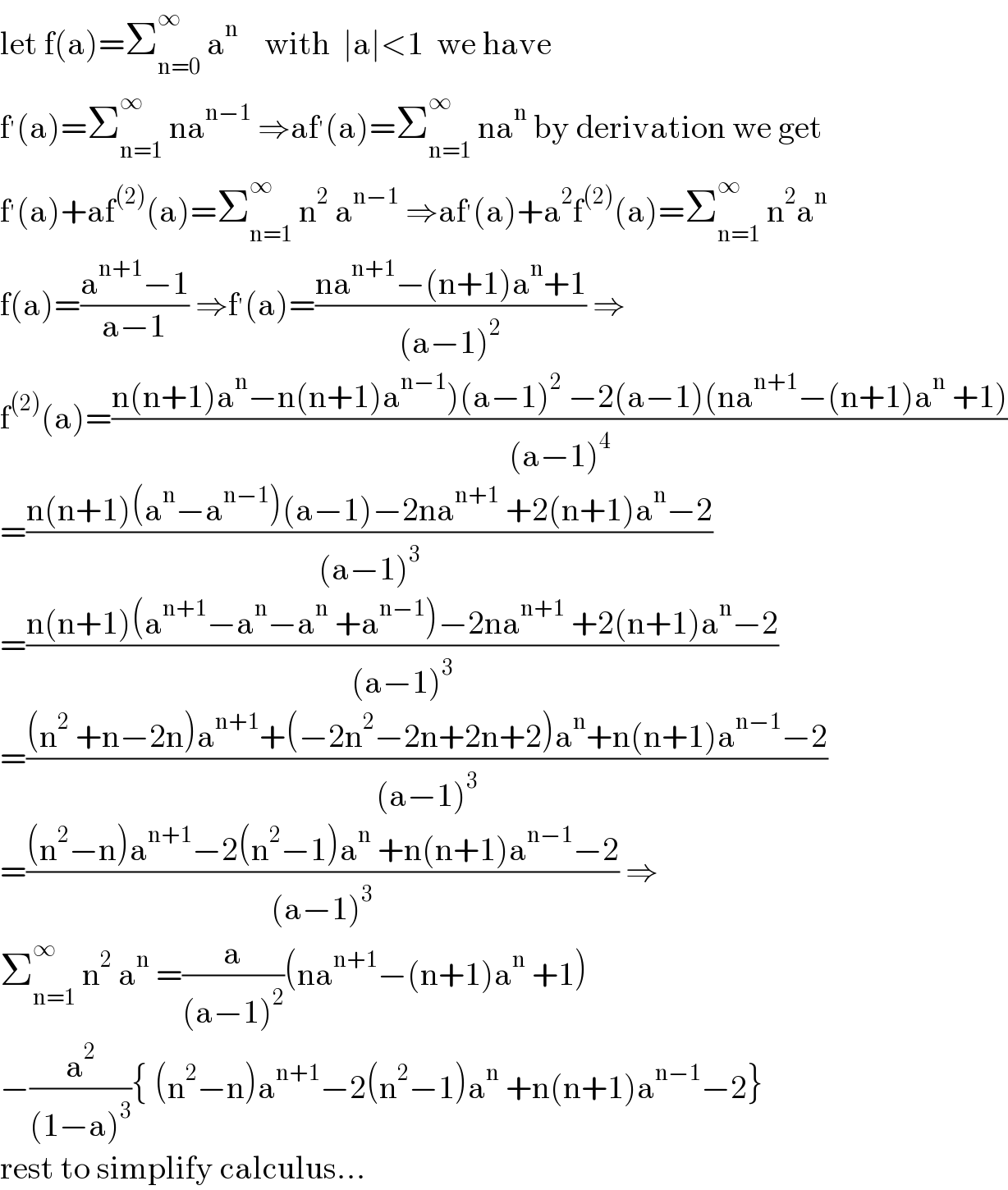
let f(a)=Σ_(n=0) ^∞ a^n with ∣a∣<1 we have f^′ (a)=Σ_(n=1) ^∞ na^(n−1) ⇒af^′ (a)=Σ_(n=1) ^∞ na^n by derivation we get f^′ (a)+af^((2)) (a)=Σ_(n=1) ^∞ n^2 a^(n−1) ⇒af^′ (a)+a^2 f^((2)) (a)=Σ_(n=1) ^∞ n^2 a^n f(a)=((a^(n+1) −1)/(a−1)) ⇒f^′ (a)=((na^(n+1) −(n+1)a^n +1)/((a−1)^2 )) ⇒ f^((2)) (a)=((n(n+1)a^n −n(n+1)a^(n−1) )(a−1)^2 −2(a−1)(na^(n+1) −(n+1)a^n +1))/((a−1)^4 )) =((n(n+1)(a^n −a^(n−1) )(a−1)−2na^(n+1) +2(n+1)a^n −2)/((a−1)^3 )) =((n(n+1)(a^(n+1) −a^n −a^n +a^(n−1) )−2na^(n+1) +2(n+1)a^n −2)/((a−1)^3 )) =(((n^2 +n−2n)a^(n+1) +(−2n^2 −2n+2n+2)a^n +n(n+1)a^(n−1) −2)/((a−1)^3 )) =(((n^2 −n)a^(n+1) −2(n^2 −1)a^n +n(n+1)a^(n−1) −2)/((a−1)^3 )) ⇒ Σ_(n=1) ^∞ n^2 a^n =(a/((a−1)^2 ))(na^(n+1) −(n+1)a^n +1) −(a^2 /((1−a)^3 )){ (n^2 −n)a^(n+1) −2(n^2 −1)a^n +n(n+1)a^(n−1) −2} rest to simplify calculus...

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{a}^{\mathrm{n}} \:\:\:\:\mathrm{with}\:\:\mid\mathrm{a}\mid<\mathrm{1}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{na}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\mathrm{af}^{'} \left(\mathrm{a}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{na}^{\mathrm{n}} \:\mathrm{by}\:\mathrm{derivation}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)+\mathrm{af}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}^{\mathrm{2}} \:\mathrm{a}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\mathrm{af}^{'} \left(\mathrm{a}\right)+\mathrm{a}^{\mathrm{2}} \mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}^{\mathrm{2}} \mathrm{a}^{\mathrm{n}} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{a}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{a}−\mathrm{1}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\mathrm{na}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} +\mathrm{1}}{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{a}\right)=\frac{\left.\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} −\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}−\mathrm{1}} \right)\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{2}\left(\mathrm{a}−\mathrm{1}\right)\left(\mathrm{na}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} \:+\mathrm{1}\right)}{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{a}^{\mathrm{n}} −\mathrm{a}^{\mathrm{n}−\mathrm{1}} \right)\left(\mathrm{a}−\mathrm{1}\right)−\mathrm{2na}^{\mathrm{n}+\mathrm{1}} \:+\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} −\mathrm{2}}{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{a}^{\mathrm{n}+\mathrm{1}} −\mathrm{a}^{\mathrm{n}} −\mathrm{a}^{\mathrm{n}} \:+\mathrm{a}^{\mathrm{n}−\mathrm{1}} \right)−\mathrm{2na}^{\mathrm{n}+\mathrm{1}} \:+\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} −\mathrm{2}}{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}−\mathrm{2n}\right)\mathrm{a}^{\mathrm{n}+\mathrm{1}} +\left(−\mathrm{2n}^{\mathrm{2}} −\mathrm{2n}+\mathrm{2n}+\mathrm{2}\right)\mathrm{a}^{\mathrm{n}} +\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}−\mathrm{1}} −\mathrm{2}}{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{n}^{\mathrm{2}} −\mathrm{n}\right)\mathrm{a}^{\mathrm{n}+\mathrm{1}} −\mathrm{2}\left(\mathrm{n}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} \:+\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}−\mathrm{1}} −\mathrm{2}}{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}^{\mathrm{2}} \:\mathrm{a}^{\mathrm{n}} \:=\frac{\mathrm{a}}{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{na}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} \:+\mathrm{1}\right) \\ $$$$−\frac{\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{a}\right)^{\mathrm{3}} }\left\{\:\left(\mathrm{n}^{\mathrm{2}} −\mathrm{n}\right)\mathrm{a}^{\mathrm{n}+\mathrm{1}} −\mathrm{2}\left(\mathrm{n}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{a}^{\mathrm{n}} \:+\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{a}^{\mathrm{n}−\mathrm{1}} −\mathrm{2}\right\} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{simplify}\:\mathrm{calculus}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply