Question Number 147587 by mathdanisur last updated on 22/Jul/21
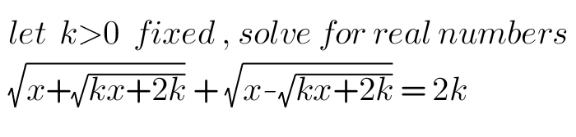
Commented by ajfour last updated on 22/Jul/21
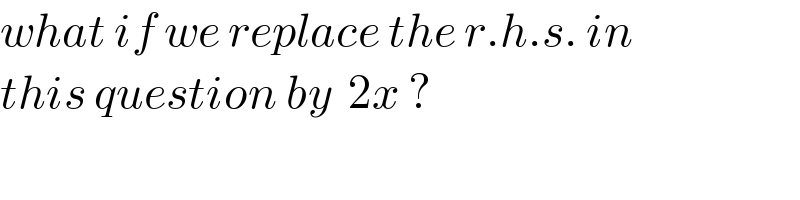
$${what}\:{if}\:{we}\:{replace}\:{the}\:{r}.{h}.{s}.\:{in} \\ $$$${this}\:{question}\:{by}\:\:\mathrm{2}{x}\:? \\ $$
Answered by iloveisrael last updated on 22/Jul/21
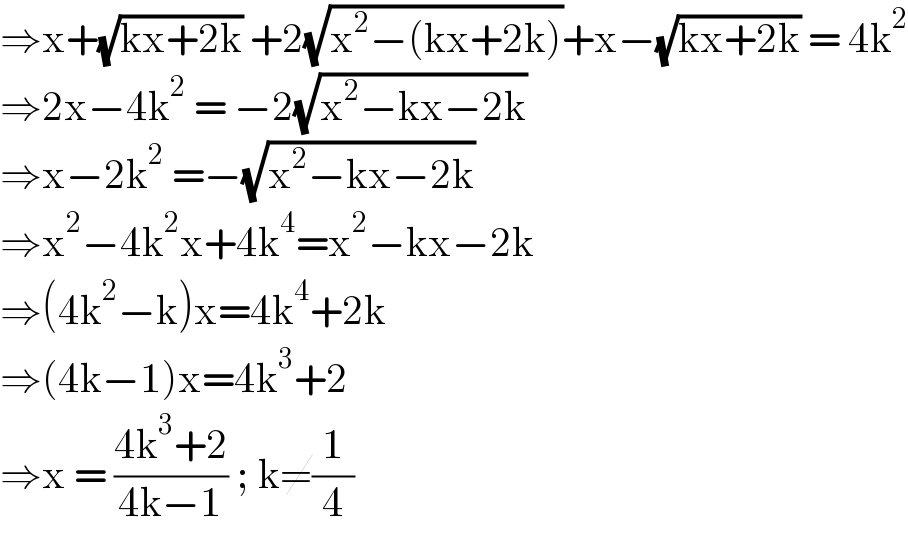
$$\Rightarrow\mathrm{x}+\sqrt{\mathrm{kx}+\mathrm{2k}}\:+\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\left(\mathrm{kx}+\mathrm{2k}\right)}+\mathrm{x}−\sqrt{\mathrm{kx}+\mathrm{2k}}\:=\:\mathrm{4k}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2x}−\mathrm{4k}^{\mathrm{2}} \:=\:−\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{kx}−\mathrm{2k}} \\ $$$$\Rightarrow\mathrm{x}−\mathrm{2k}^{\mathrm{2}} \:=−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{kx}−\mathrm{2k}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4k}^{\mathrm{2}} \mathrm{x}+\mathrm{4k}^{\mathrm{4}} =\mathrm{x}^{\mathrm{2}} −\mathrm{kx}−\mathrm{2k} \\ $$$$\Rightarrow\left(\mathrm{4k}^{\mathrm{2}} −\mathrm{k}\right)\mathrm{x}=\mathrm{4k}^{\mathrm{4}} +\mathrm{2k} \\ $$$$\Rightarrow\left(\mathrm{4k}−\mathrm{1}\right)\mathrm{x}=\mathrm{4k}^{\mathrm{3}} +\mathrm{2} \\ $$$$\Rightarrow\mathrm{x}\:=\:\frac{\mathrm{4k}^{\mathrm{3}} +\mathrm{2}}{\mathrm{4k}−\mathrm{1}}\:;\:\mathrm{k}\neq\frac{\mathrm{1}}{\mathrm{4}}\: \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$
