Question-147623

Question Number 147623 by mari last updated on 22/Jul/21

Commented by tabata last updated on 22/Jul/21

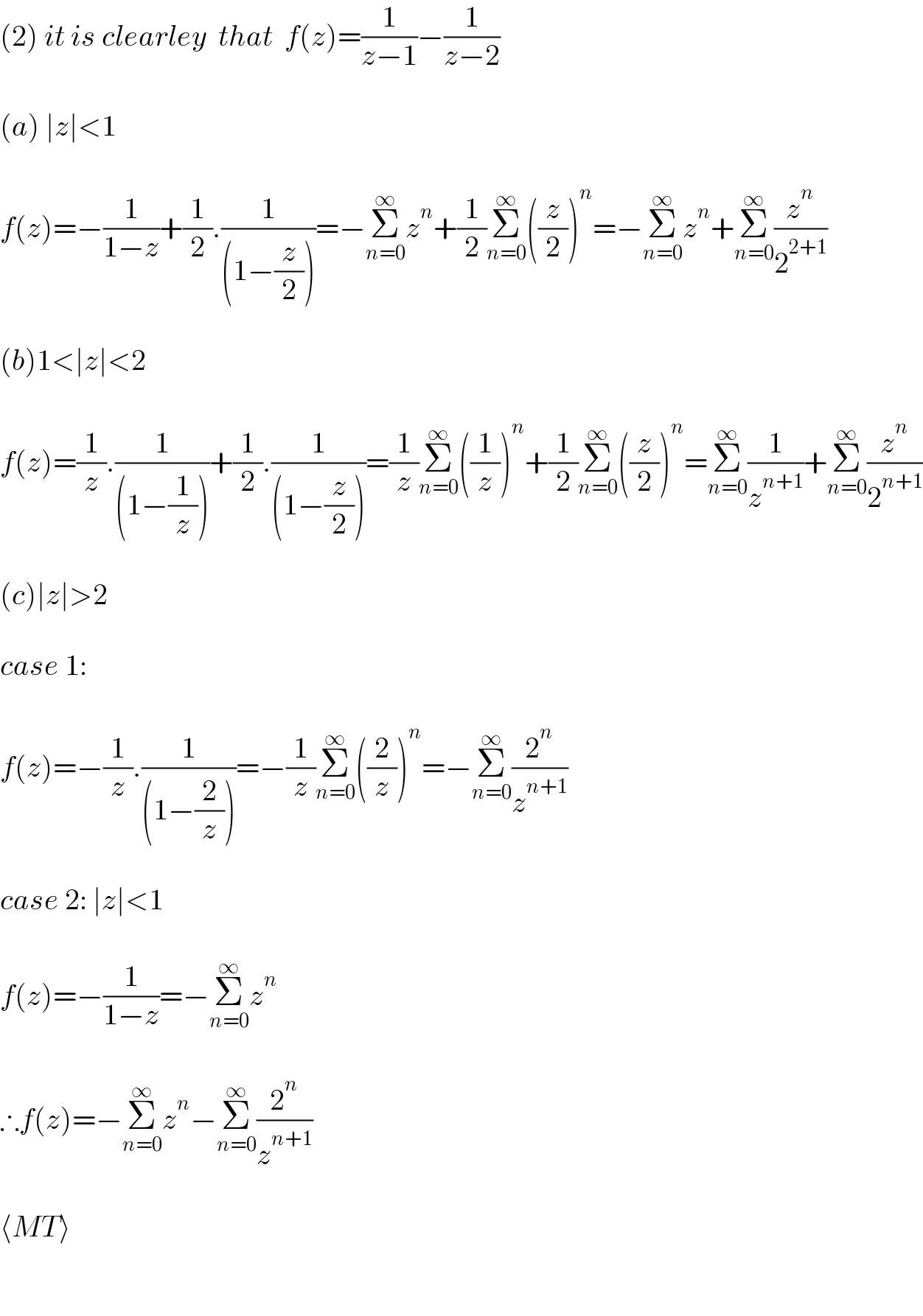
(2) it is clearley that f(z)=(1/(z−1))−(1/(z−2)) (a) ∣z∣<1 f(z)=−(1/(1−z))+(1/2).(1/((1−(z/2))))=−Σ_(n=0) ^∞ z^n +(1/2)Σ_(n=0) ^∞ ((z/2))^n =−Σ_(n=0) ^∞ z^n +Σ_(n=0) ^∞ (z^n /2^(2+1) ) (b)1<∣z∣<2 f(z)=(1/z).(1/((1−(1/z))))+(1/2).(1/((1−(z/2))))=(1/z)Σ_(n=0) ^∞ ((1/z))^n +(1/2)Σ_(n=0) ^∞ ((z/2))^n =Σ_(n=0) ^∞ (1/z^(n+1) )+Σ_(n=0) ^∞ (z^n /2^(n+1) ) (c)∣z∣>2 case 1: f(z)=−(1/z).(1/((1−(2/z))))=−(1/z)Σ_(n=0) ^∞ ((2/z))^n =−Σ_(n=0) ^∞ (2^n /z^(n+1) ) case 2: ∣z∣<1 f(z)=−(1/(1−z))=−Σ_(n=0) ^∞ z^n ∴f(z)=−Σ_(n=0) ^∞ z^n −Σ_(n=0) ^∞ (2^n /z^(n+1) ) ⟨MT⟩

$$\left(\mathrm{2}\right)\:{it}\:{is}\:{clearley}\:\:{that}\:\:{f}\left({z}\right)=\frac{\mathrm{1}}{{z}−\mathrm{1}}−\frac{\mathrm{1}}{{z}−\mathrm{2}} \\ $$$$ \\ $$$$\left({a}\right)\:\mid{z}\mid<\mathrm{1} \\ $$$$ \\ $$$${f}\left({z}\right)=−\frac{\mathrm{1}}{\mathrm{1}−{z}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{{z}}{\mathrm{2}}\right)}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{z}^{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{z}}{\mathrm{2}}\right)^{{n}} =−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{z}^{{n}} +\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{z}^{{n}} }{\mathrm{2}^{\mathrm{2}+\mathrm{1}} } \\ $$$$ \\ $$$$\left({b}\right)\mathrm{1}<\mid{z}\mid<\mathrm{2} \\ $$$$ \\ $$$${f}\left({z}\right)=\frac{\mathrm{1}}{{z}}.\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{\mathrm{1}}{{z}}\right)}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{{z}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{{z}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{z}}\right)^{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{z}}{\mathrm{2}}\right)^{{n}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{z}^{{n}+\mathrm{1}} }+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{z}^{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$ \\ $$$$\left({c}\right)\mid{z}\mid>\mathrm{2} \\ $$$$ \\ $$$${case}\:\mathrm{1}: \\ $$$$ \\ $$$${f}\left({z}\right)=−\frac{\mathrm{1}}{{z}}.\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{\mathrm{2}}{{z}}\right)}=−\frac{\mathrm{1}}{{z}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{2}}{{z}}\right)^{{n}} =−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{{z}^{{n}+\mathrm{1}} } \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:\mid{z}\mid<\mathrm{1}\: \\ $$$$ \\ $$$${f}\left({z}\right)=−\frac{\mathrm{1}}{\mathrm{1}−{z}}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{z}^{{n}} \: \\ $$$$ \\ $$$$\therefore{f}\left({z}\right)=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{z}^{{n}} −\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{{z}^{{n}+\mathrm{1}} } \\ $$$$ \\ $$$$\langle{MT}\rangle \\ $$$$\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply