Menu Close

Question-147778

Tinku Tara 0 Comments
Pin




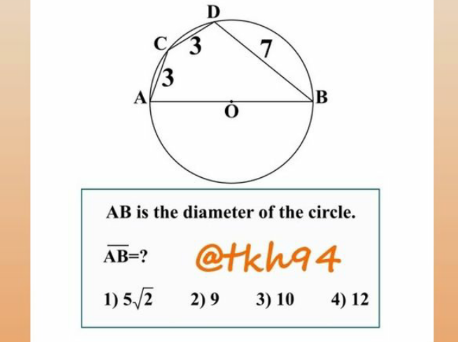
Question Number 147778 by mnjuly1970 last updated on 23/Jul/21
Answered by liberty last updated on 23/Jul/21
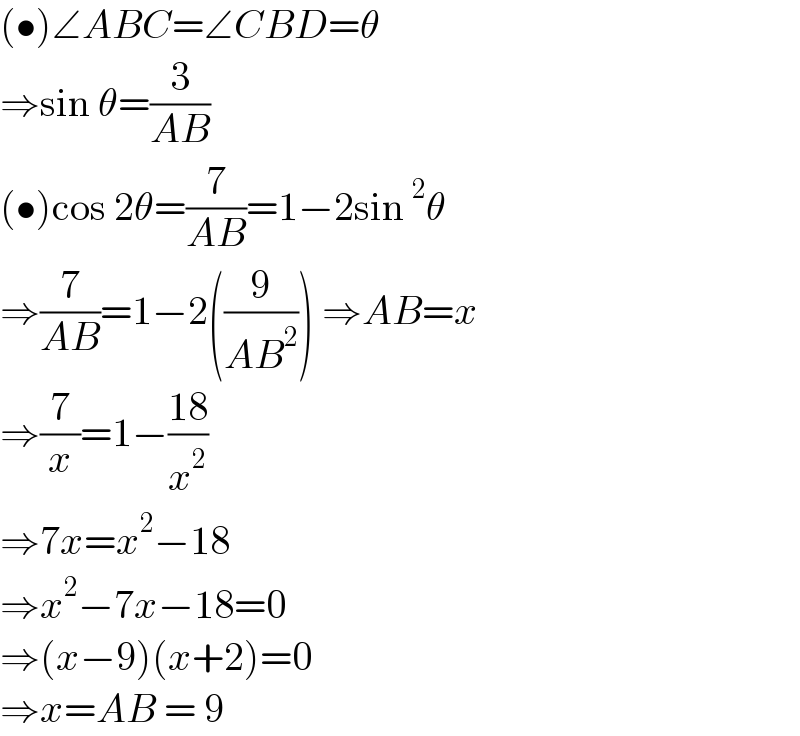
(•)∠ABC=∠CBD=θ ⇒sin θ=(3/(AB)) (•)cos 2θ=(7/(AB))=1−2sin^2 θ ⇒(7/(AB))=1−2((9/(AB^2 ))) ⇒AB=x ⇒(7/x)=1−((18)/x^2 ) ⇒7x=x^2 −18 ⇒x^2 −7x−18=0 ⇒(x−9)(x+2)=0 ⇒x=AB = 9
$$\left(\bullet\right)\angle{ABC}=\angle{CBD}=\theta \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{3}}{{AB}}\: \\ $$$$\left(\bullet\right)\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{7}}{{AB}}=\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\frac{\mathrm{7}}{{AB}}=\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{9}}{{AB}^{\mathrm{2}} }\right)\:\Rightarrow{AB}={x} \\ $$$$\Rightarrow\frac{\mathrm{7}}{{x}}=\mathrm{1}−\frac{\mathrm{18}}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{7}{x}={x}^{\mathrm{2}} −\mathrm{18}\: \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{18}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{9}\right)\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}={AB}\:=\:\mathrm{9} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Jul/21
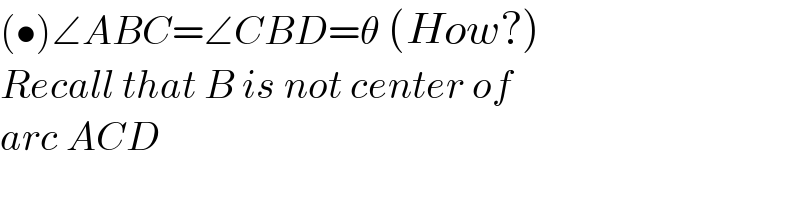
(•)∠ABC=∠CBD=θ (How?) Recall that B is not center of arc ACD
$$\left(\bullet\right)\angle{ABC}=\angle{CBD}=\theta\:\left({How}?\right) \\ $$$${Recall}\:{that}\:{B}\:{is}\:{not}\:{center}\:{of}\: \\ $$$${arc}\:{ACD} \\ $$
Commented by mnjuly1970 last updated on 23/Jul/21
thanks alot mr liberty.. nice solution...
$${thanks}\:{alot}\:{mr}\:{liberty}.. \\ $$$${nice}\:{solution}… \\ $$
Answered by Rasheed.Sindhi last updated on 24/Jul/21
Let the radius is r,∠AOC=θ ⇒∠COD=θ⇒BOD=2θ △AOC: AC^2 =r^2 +r^2 −2r^2 cos ∠AOC=3^2 =9 2r^2 −2r^2 cos θ=9 2r^2 (1−cos θ)=9 1−cos θ=(9/(2r^2 )) cos θ=1−(9/(2r^2 ))=((2r^2 −9)/(2r^2 )) △BOD: BD^2 =r^2 +r^2 −2r^2 cos∠BOD=7^2 =49 2r^2 −2r^2 cos(π−2θ)=49 determinant (((cos(π−θ)=−cos θ ))) 2r^2 −2r^2 (−cos(2θ))=49 2r^2 +2r^2 cos(2θ)=49 determinant (((cos(2θ)=2cos^2 θ−1 ))) 2r^2 +2r^2 (2cos^2 θ−1)=49 2cos^2 θ=((49)/(2r^2 )) (((2r^2 −9)/(2r^2 )))^2 =((49)/(4r^2 )) (((2r^2 −9)^2 )/(4r^4 ))=((49)/(4r^2 )) ((2r^2 −9)/(2r^2 ))=(7/(2r)) ((2r^2 −9)/r)=7 2r^2 −7r−9=0 2r^2 −9r+2r−9=0 r(2r−9)+1(2r−9)=0 (r+1)(2r−9)=0 r=−9(rejectable) r=9/2 AB=2r=9
$${Let}\:{the}\:{radius}\:{is}\:\boldsymbol{{r}},\angle{AOC}=\theta \\ $$$$\Rightarrow\angle{COD}=\theta\Rightarrow{BOD}=\mathrm{2}\theta \\ $$$$\bigtriangleup{AOC}: \\ $$$${AC}^{\mathrm{2}} =\boldsymbol{{r}}^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \mathrm{cos}\:\angle{AOC}=\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \mathrm{cos}\:\theta=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−\mathrm{cos}\:\theta=\frac{\mathrm{9}}{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\theta=\mathrm{1}−\frac{\mathrm{9}}{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} }=\frac{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{9}}{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\: \\ $$$$\bigtriangleup{BOD}: \\ $$$${BD}^{\mathrm{2}} =\boldsymbol{{r}}^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \mathrm{cos}\angle{BOD}=\mathrm{7}^{\mathrm{2}} =\mathrm{49} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \mathrm{cos}\left(\pi−\mathrm{2}\theta\right)=\mathrm{49} \\ $$$$\:\:\:\:\:\:\:\:\:\begin{array}{|c|}{\mathrm{cos}\left(\pi−\theta\right)=−\mathrm{cos}\:\theta\:\:}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \left(−\mathrm{cos}\left(\mathrm{2}\theta\right)\right)=\mathrm{49} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{2}\theta\right)=\mathrm{49} \\ $$$$\:\:\:\:\:\:\:\:\:\begin{array}{|c|}{\mathrm{cos}\left(\mathrm{2}\theta\right)=\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{1}\:\:}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \left(\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{1}\right)=\mathrm{49} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2cos}^{\mathrm{2}} \theta=\frac{\mathrm{49}}{\mathrm{2}{r}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{9}}{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} }\right)^{\mathrm{2}} =\frac{\mathrm{49}}{\mathrm{4}\boldsymbol{{r}}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\left(\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }{\mathrm{4}\boldsymbol{{r}}^{\mathrm{4}} }=\frac{\mathrm{49}}{\mathrm{4}\boldsymbol{{r}}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{9}}{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}\boldsymbol{{r}}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{9}}{\boldsymbol{{r}}}=\mathrm{7} \\ $$$$\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{7}\boldsymbol{{r}}−\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{9}\boldsymbol{{r}}+\mathrm{2}\boldsymbol{{r}}−\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\boldsymbol{{r}}\left(\mathrm{2}\boldsymbol{{r}}−\mathrm{9}\right)+\mathrm{1}\left(\mathrm{2}\boldsymbol{{r}}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\left(\boldsymbol{{r}}+\mathrm{1}\right)\left(\mathrm{2}\boldsymbol{{r}}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\boldsymbol{{r}}=−\mathrm{9}\left({rejectable}\right) \\ $$$$\:\:\:\:\:\boldsymbol{{r}}=\mathrm{9}/\mathrm{2} \\ $$$$\:\:\:\:{AB}=\mathrm{2}{r}=\mathrm{9} \\ $$
Commented by mnjuly1970 last updated on 23/Jul/21
tashakor sir Rasheed...
$$\:\:\:{tashakor}\:{sir}\:{Rasheed}… \\ $$
Answered by mr W last updated on 24/Jul/21
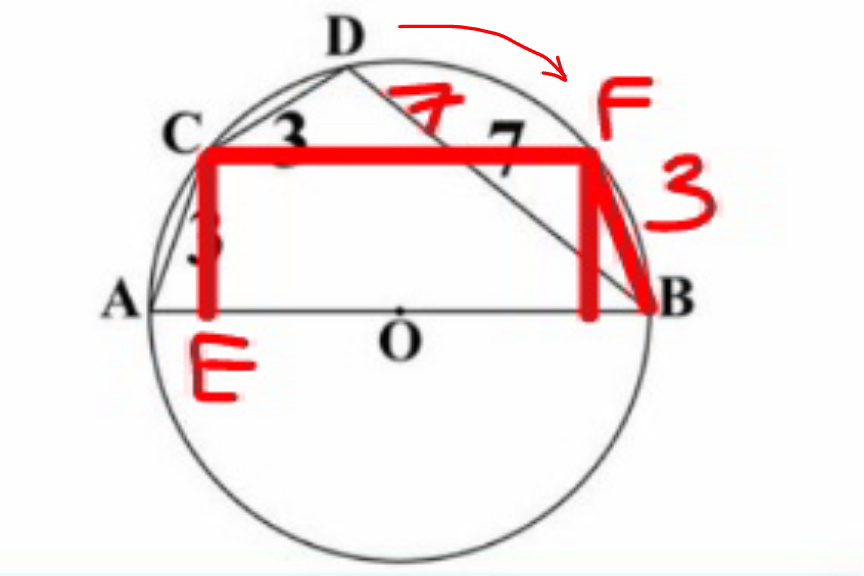
Commented by mr W last updated on 23/Jul/21
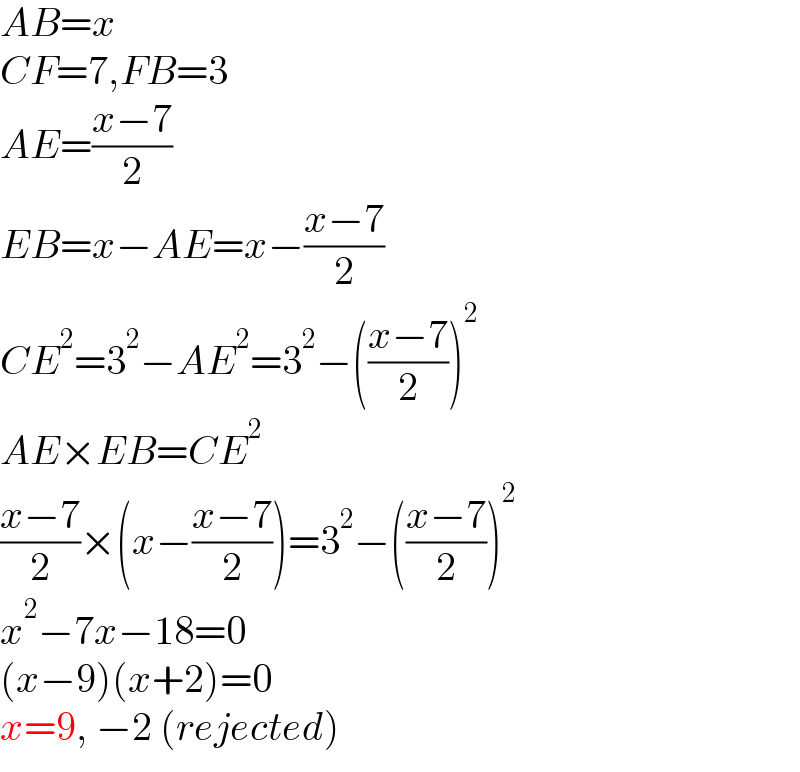
AB=x CF=7,FB=3 AE=((x−7)/2) EB=x−AE=x−((x−7)/2) CE^2 =3^2 −AE^2 =3^2 −(((x−7)/2))^2 AE×EB=CE^2 ((x−7)/2)×(x−((x−7)/2))=3^2 −(((x−7)/2))^2 x^2 −7x−18=0 (x−9)(x+2)=0 x=9, −2 (rejected)
$${AB}={x} \\ $$$${CF}=\mathrm{7},{FB}=\mathrm{3} \\ $$$${AE}=\frac{{x}−\mathrm{7}}{\mathrm{2}} \\ $$$${EB}={x}−{AE}={x}−\frac{{x}−\mathrm{7}}{\mathrm{2}} \\ $$$${CE}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} −{AE}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} −\left(\frac{{x}−\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${AE}×{EB}={CE}^{\mathrm{2}} \\ $$$$\frac{{x}−\mathrm{7}}{\mathrm{2}}×\left({x}−\frac{{x}−\mathrm{7}}{\mathrm{2}}\right)=\mathrm{3}^{\mathrm{2}} −\left(\frac{{x}−\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{18}=\mathrm{0} \\ $$$$\left({x}−\mathrm{9}\right)\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$${x}=\mathrm{9},\:−\mathrm{2}\:\left({rejected}\right) \\ $$
Commented by Tawa11 last updated on 03/Aug/21
great
$$\mathrm{great} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *