Menu Close

Question-147795

Tinku Tara 0 Comments
Pin




Question Number 147795 by ajfour last updated on 23/Jul/21
Commented by ajfour last updated on 23/Jul/21
Find b/a.
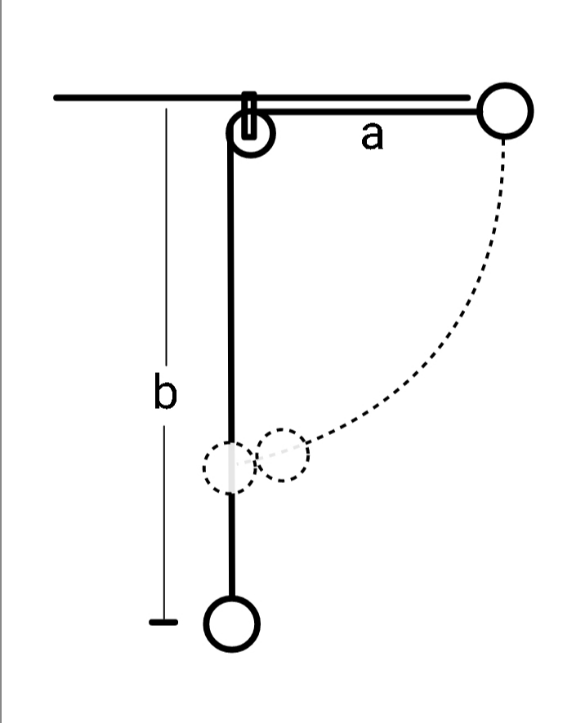
$${Find}\:{b}/{a}. \\ $$
Commented by mr W last updated on 24/Jul/21
very nice question! i have tried to find an answer. but it′s not so easy to me.
$${very}\:{nice}\:{question}! \\ $$$${i}\:{have}\:{tried}\:{to}\:{find}\:{an}\:{answer}.\:{but} \\ $$$${it}'{s}\:{not}\:{so}\:{easy}\:{to}\:{me}. \\ $$
Answered by mr W last updated on 23/Jul/21
Commented by mr W last updated on 24/Jul/21
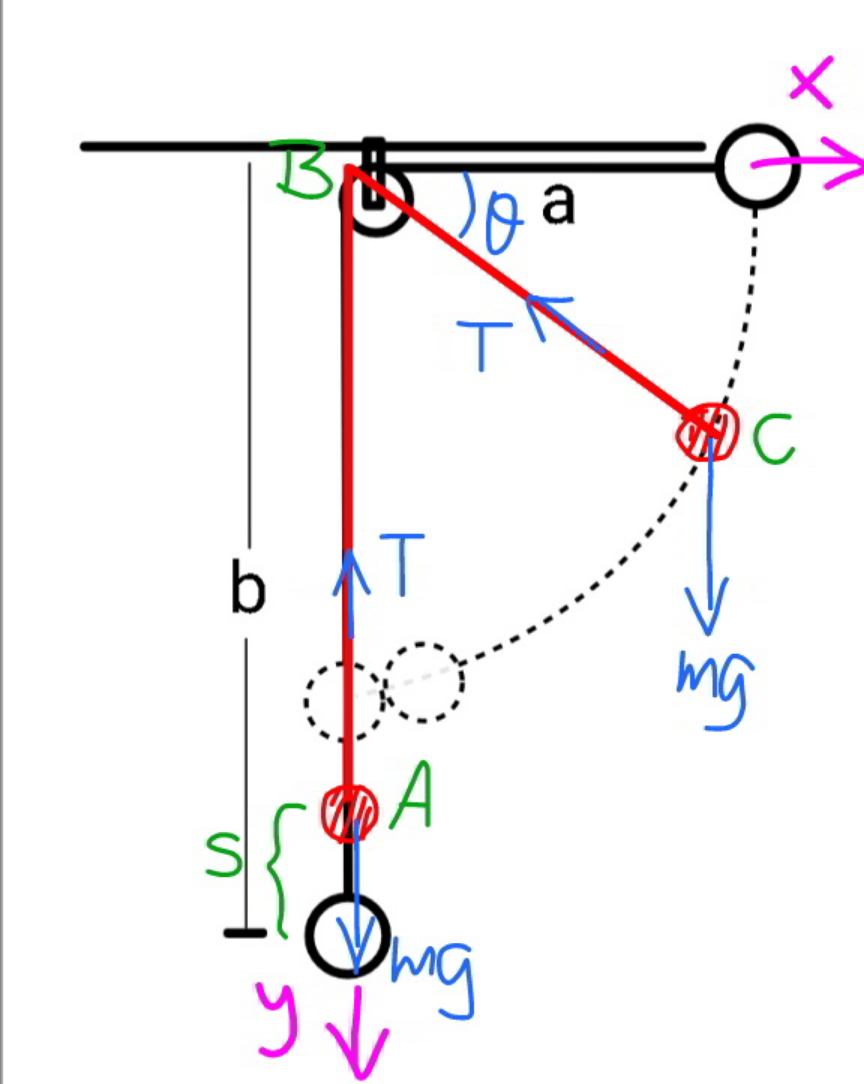
y_A =b−s x_C =(a+s)cos θ y_C =(a+s)sin θ ω=(dθ/dt) u=(ds/dt) u_A =−(dy_A /dt)=u a_A =(du_A /dt)=(du/dt) T−mg=ma_A ⇒T=m(a_A +g) u_(Cx) =−(dx_C /dt)=(a+s)ωsin θ−ucos θ a_(Cx) =uωsin θ+(a+s)αsin θ+(a+s)ω^2 cos θ−a_A cos θ+uωsin θ u_(Cy) =(dy_C /dt)=(a+s)ωcos θ+usin θ a_(Cy) =uωcos θ+(a+s)αcos θ−(a+s)ω^2 sin θ+a_A sin θ+uωcos θ (1/2)m[u^2 +(a+s)^2 ω^2 sin^2 θ+u^2 cos^2 θ−2(a+s)ωusin θcos θ+(a+s)^2 ω^2 cos^2 θ+u^2 sin^2 θ+2(a+s)ωucos θsin θ]=mg[(a+s)sin θ−s] ⇒2u^2 +(a+s)^2 ω^2 =2g[(a+s)sin θ−s] ...(i) Tcos θ=ma_(Cx) (a_A +g)cos θ=uωsin θ+(a+s)αsin θ+(a+s)ω^2 cos θ−a_A cos θ+uωsin θ ⇒2a_A +g=2uωtan θ+(a+s)αtan θ+(a+s)ω^2 mg−Tsin θ=ma_(Cy) ⇒2a_A +g=(1/(tan θ))[g−2uω−(a+s)α]+(a+s)ω^2 2uωtan θ+(a+s)αtan θ+(a+s)ω^2 =(1/(tan θ))[g−2uω−(a+s)α]+(a+s)ω^2 [2uω+(a+s)α](1+tan^2 θ)=g ⇒2uω+(a+s)α=gcos^2 θ ...(ii) α=(dω/dt)=ω(dω/dθ) from (i): u=(√(g[(a+s)sin θ−s]−(1/2)(a+s)^2 ω^2 )) ⇒(ds/dθ)=(1/ω)(√(g[(a+s)sin θ−s]−(1/2)(a+s)^2 ω^2 )) from (ii): ⇒(dω/dθ)=((gcos^2 θ)/(ω(a+s)))−(2/(a+s))(√(g[(a+s)sin θ−s]−(1/2)(a+s)^2 ω^2 )) ...... s(θ)∣_(θ=0) =0 ω(θ)∣_(θ=0) =0 s(θ)∣_(θ=(π/2)) =((b−a)/2)
$${y}_{{A}} ={b}−{s} \\ $$$${x}_{{C}} =\left({a}+{s}\right)\mathrm{cos}\:\theta \\ $$$${y}_{{C}} =\left({a}+{s}\right)\mathrm{sin}\:\theta \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$${u}=\frac{{ds}}{{dt}} \\ $$$${u}_{{A}} =−\frac{{dy}_{{A}} }{{dt}}={u} \\ $$$${a}_{{A}} =\frac{{du}_{{A}} }{{dt}}=\frac{{du}}{{dt}} \\ $$$${T}−{mg}={ma}_{{A}} \\ $$$$\Rightarrow{T}={m}\left({a}_{{A}} +{g}\right) \\ $$$${u}_{{Cx}} =−\frac{{dx}_{{C}} }{{dt}}=\left({a}+{s}\right)\omega\mathrm{sin}\:\theta−{u}\mathrm{cos}\:\theta \\ $$$${a}_{{Cx}} ={u}\omega\mathrm{sin}\:\theta+\left({a}+{s}\right)\alpha\mathrm{sin}\:\theta+\left({a}+{s}\right)\omega^{\mathrm{2}} \mathrm{cos}\:\theta−{a}_{{A}} \mathrm{cos}\:\theta+{u}\omega\mathrm{sin}\:\theta \\ $$$${u}_{{Cy}} =\frac{{dy}_{{C}} }{{dt}}=\left({a}+{s}\right)\omega\mathrm{cos}\:\theta+{u}\mathrm{sin}\:\theta \\ $$$${a}_{{Cy}} ={u}\omega\mathrm{cos}\:\theta+\left({a}+{s}\right)\alpha\mathrm{cos}\:\theta−\left({a}+{s}\right)\omega^{\mathrm{2}} \mathrm{sin}\:\theta+{a}_{{A}} \mathrm{sin}\:\theta+{u}\omega\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{m}\left[{u}^{\mathrm{2}} +\left({a}+{s}\right)^{\mathrm{2}} \omega^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{u}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}\left({a}+{s}\right)\omega{u}\mathrm{sin}\:\theta\mathrm{cos}\:\theta+\left({a}+{s}\right)^{\mathrm{2}} \omega^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{u}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\left({a}+{s}\right)\omega{u}\mathrm{cos}\:\theta\mathrm{sin}\:\theta\right]={mg}\left[\left({a}+{s}\right)\mathrm{sin}\:\theta−{s}\right] \\ $$$$\Rightarrow\mathrm{2}{u}^{\mathrm{2}} +\left({a}+{s}\right)^{\mathrm{2}} \omega^{\mathrm{2}} =\mathrm{2}{g}\left[\left({a}+{s}\right)\mathrm{sin}\:\theta−{s}\right]\:\:\:…\left({i}\right) \\ $$$${T}\mathrm{cos}\:\theta={ma}_{{Cx}} \\ $$$$\left({a}_{{A}} +{g}\right)\mathrm{cos}\:\theta={u}\omega\mathrm{sin}\:\theta+\left({a}+{s}\right)\alpha\mathrm{sin}\:\theta+\left({a}+{s}\right)\omega^{\mathrm{2}} \mathrm{cos}\:\theta−{a}_{{A}} \mathrm{cos}\:\theta+{u}\omega\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{2}{a}_{{A}} +{g}=\mathrm{2}{u}\omega\mathrm{tan}\:\theta+\left({a}+{s}\right)\alpha\mathrm{tan}\:\theta+\left({a}+{s}\right)\omega^{\mathrm{2}} \\ $$$${mg}−{T}\mathrm{sin}\:\theta={ma}_{{Cy}} \\ $$$$\Rightarrow\mathrm{2}{a}_{{A}} +{g}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta}\left[{g}−\mathrm{2}{u}\omega−\left({a}+{s}\right)\alpha\right]+\left({a}+{s}\right)\omega^{\mathrm{2}} \\ $$$$\mathrm{2}{u}\omega\mathrm{tan}\:\theta+\left({a}+{s}\right)\alpha\mathrm{tan}\:\theta+\left({a}+{s}\right)\omega^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{tan}\:\theta}\left[{g}−\mathrm{2}{u}\omega−\left({a}+{s}\right)\alpha\right]+\left({a}+{s}\right)\omega^{\mathrm{2}} \\ $$$$\left[\mathrm{2}{u}\omega+\left({a}+{s}\right)\alpha\right]\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)={g} \\ $$$$\Rightarrow\mathrm{2}{u}\omega+\left({a}+{s}\right)\alpha={g}\mathrm{cos}^{\mathrm{2}} \:\theta\:\:\:…\left({ii}\right) \\ $$$$\alpha=\frac{{d}\omega}{{dt}}=\omega\frac{{d}\omega}{{d}\theta} \\ $$$${from}\:\left({i}\right): \\ $$$${u}=\sqrt{{g}\left[\left({a}+{s}\right)\mathrm{sin}\:\theta−{s}\right]−\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{s}\right)^{\mathrm{2}} \omega^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{ds}}{{d}\theta}=\frac{\mathrm{1}}{\omega}\sqrt{{g}\left[\left({a}+{s}\right)\mathrm{sin}\:\theta−{s}\right]−\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{s}\right)^{\mathrm{2}} \omega^{\mathrm{2}} } \\ $$$${from}\:\left({ii}\right): \\ $$$$\Rightarrow\frac{{d}\omega}{{d}\theta}=\frac{{g}\mathrm{cos}^{\mathrm{2}} \:\theta}{\omega\left({a}+{s}\right)}−\frac{\mathrm{2}}{{a}+{s}}\sqrt{{g}\left[\left({a}+{s}\right)\mathrm{sin}\:\theta−{s}\right]−\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{s}\right)^{\mathrm{2}} \omega^{\mathrm{2}} } \\ $$$$…… \\ $$$${s}\left(\theta\right)\mid_{\theta=\mathrm{0}} =\mathrm{0} \\ $$$$\omega\left(\theta\right)\mid_{\theta=\mathrm{0}} =\mathrm{0} \\ $$$${s}\left(\theta\right)\mid_{\theta=\frac{\pi}{\mathrm{2}}} =\frac{{b}−{a}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 25/Jul/21
mgrcos θ=(mr^2 )((ωdω)/dθ) ...(i) mgrsin θ=(1/2)m(v^2 +v^2 ) +(1/2)m(ωr)^2 +mg(a+b−r) ..(ii) v=(dr/dt)=((ωdr)/dθ) ...(iii) L=a+b ⇒ 2g(rsin θ+r−L) =2(((ωdr)/dθ))^2 +(ωr)^2 ⇒ ω^2 =((2g(rsin θ+r−L))/(2((dr/dθ))^2 +r^2 )) ((2ωdω)/dθ)=((2g((dr/dθ)sin θ+rcos θ+(dr/dθ)){2((dr/dθ))^2 +r^2 }−2g(rsin θ+r−L){4((dr/dθ))((d^2 r/dθ^2 ))+2r((dr/dθ))^2 })/({2((dr/dθ))^2 +r^2 }^2 )) =((2gcos θ)/r) ⇒ (((rdr)/dθ))(1+sin θ) +r^2 cos θ{2((dr/dθ))^2 +r^2 } −(r^2 sin θ+r^2 −Lr){4((dr/dθ))((d^2 r/dθ^2 ))+2r((dr/dθ))^2 } = cos θ{2((dr/dθ))^2 +r^2 }^2 difficult D.E. , sir.
$${mgr}\mathrm{cos}\:\theta=\left({mr}^{\mathrm{2}} \right)\frac{\omega{d}\omega}{{d}\theta}\:\:…\left({i}\right) \\ $$$$ \\ $$$${mgr}\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}{m}\left({v}^{\mathrm{2}} +{v}^{\mathrm{2}} \right) \\ $$$$\:+\frac{\mathrm{1}}{\mathrm{2}}{m}\left(\omega{r}\right)^{\mathrm{2}} +{mg}\left({a}+{b}−{r}\right)\:\:..\left({ii}\right) \\ $$$${v}=\frac{{dr}}{{dt}}=\frac{\omega{dr}}{{d}\theta}\:\:\:\:…\left({iii}\right) \\ $$$${L}={a}+{b} \\ $$$$\Rightarrow \\ $$$$\mathrm{2}{g}\left({r}\mathrm{sin}\:\theta+{r}−{L}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\frac{\omega{dr}}{{d}\theta}\right)^{\mathrm{2}} +\left(\omega{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\omega^{\mathrm{2}} =\frac{\mathrm{2}{g}\left({r}\mathrm{sin}\:\theta+{r}−{L}\right)}{\mathrm{2}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}\omega{d}\omega}{{d}\theta}=\frac{\mathrm{2}{g}\left(\frac{{dr}}{{d}\theta}\mathrm{sin}\:\theta+{r}\mathrm{cos}\:\theta+\frac{{dr}}{{d}\theta}\right)\left\{\mathrm{2}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \right\}−\mathrm{2}{g}\left({r}\mathrm{sin}\:\theta+{r}−{L}\right)\left\{\mathrm{4}\left(\frac{{dr}}{{d}\theta}\right)\left(\frac{{d}^{\mathrm{2}} {r}}{{d}\theta^{\mathrm{2}} }\right)+\mathrm{2}{r}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} \right\}}{\left\{\mathrm{2}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \right\}^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{2}{g}\mathrm{cos}\:\theta}{{r}} \\ $$$$\Rightarrow \\ $$$$\left(\frac{{rdr}}{{d}\theta}\right)\left(\mathrm{1}+\mathrm{sin}\:\theta\right) \\ $$$$+{r}^{\mathrm{2}} \mathrm{cos}\:\theta\left\{\mathrm{2}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \right\} \\ $$$$−\left({r}^{\mathrm{2}} \mathrm{sin}\:\theta+{r}^{\mathrm{2}} −{Lr}\right)\left\{\mathrm{4}\left(\frac{{dr}}{{d}\theta}\right)\left(\frac{{d}^{\mathrm{2}} {r}}{{d}\theta^{\mathrm{2}} }\right)+\mathrm{2}{r}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:=\:\:\mathrm{cos}\:\theta\left\{\mathrm{2}\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$${difficult}\:{D}.{E}.\:,\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *