Question Number 147811 by mathdanisur last updated on 23/Jul/21
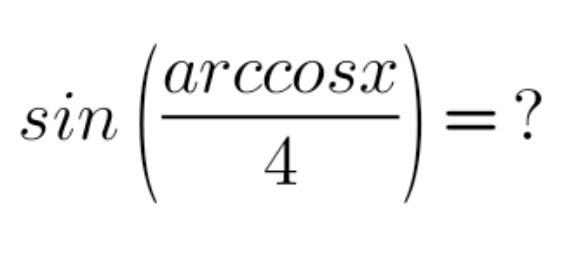
Answered by Olaf_Thorendsen last updated on 23/Jul/21

$$\mathrm{X}\:=\:\mathrm{sin}\left(\frac{\mathrm{arccos}{x}}{\mathrm{4}}\right) \\ $$$$\Rightarrow\:\mathrm{X}^{\mathrm{2}} \:=\:\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{arccos}{x}}{\mathrm{4}}\right) \\ $$$$\mathrm{X}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2}×\frac{\mathrm{arccos}{x}}{\mathrm{4}}\right)\right) \\ $$$$\mathrm{X}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\left(\frac{\mathrm{arccos}{x}}{\mathrm{2}}\right)\right) \\ $$$$\mathrm{0}\:\leqslant\:\mathrm{arccos}{x}\:\leqslant\:\pi\:\Rightarrow\:\mathrm{0}\:\leqslant\:\frac{\mathrm{arccos}{x}}{\mathrm{2}}\:\leqslant\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{X}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{arccos}{x}}{\mathrm{2}}\right)}\right) \\ $$$$\mathrm{X}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}×\frac{\mathrm{arccos}{x}}{\mathrm{2}}\right)\right.}\right) \\ $$$$\mathrm{X}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{x}\right)}\right) \\ $$$$\mathrm{X}\:=+\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\frac{{x}+\mathrm{1}}{\mathrm{2}}}\right)} \\ $$
Commented by mathdanisur last updated on 23/Jul/21

$${thank}\:{you}\:{Sir} \\ $$
