Question-147873

Question Number 147873 by 0731619 last updated on 24/Jul/21

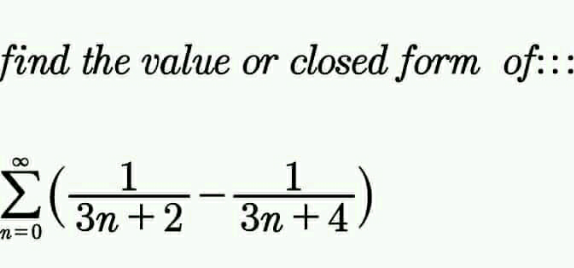
Answered by Olaf_Thorendsen last updated on 24/Jul/21

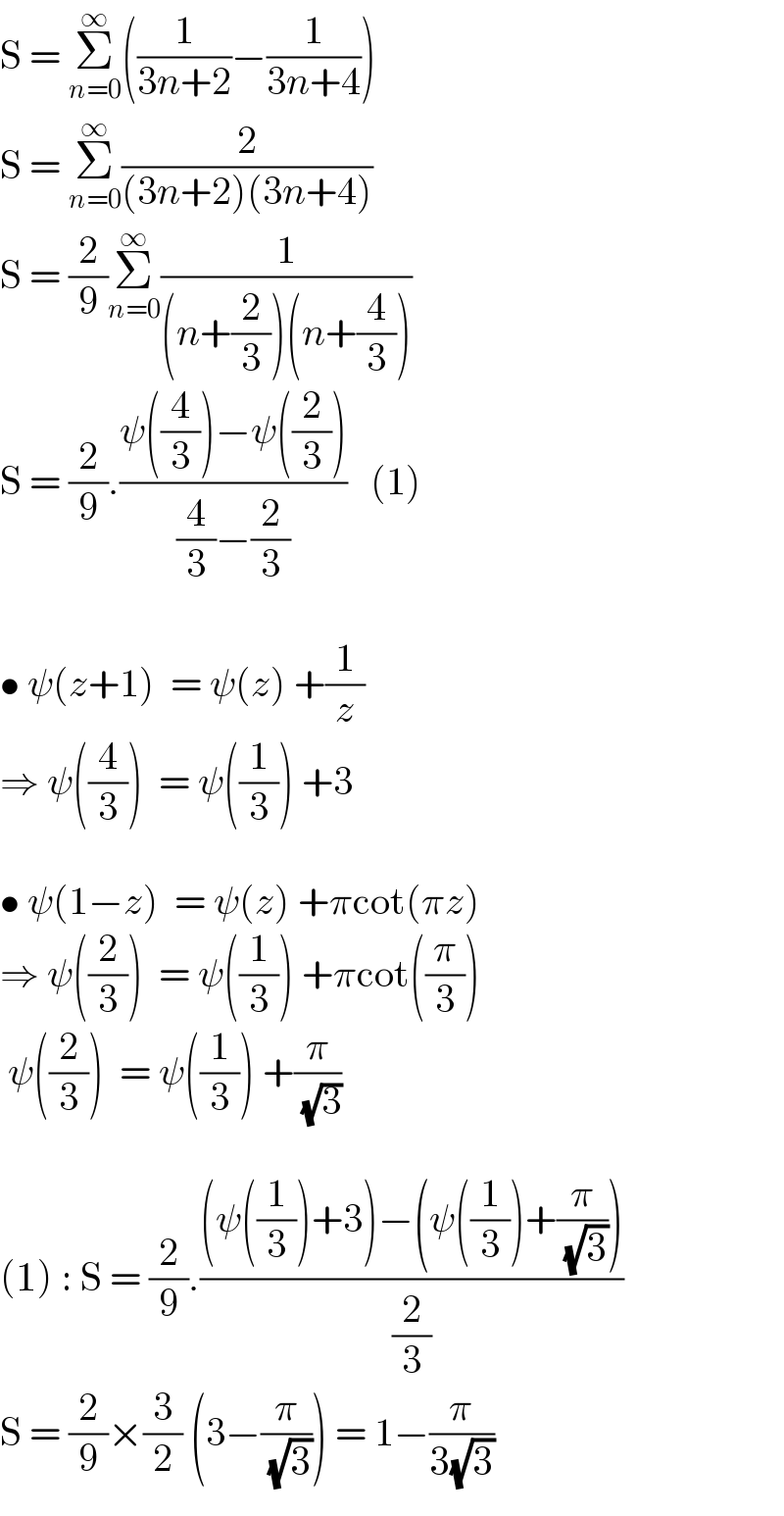
S = Σ_(n=0) ^∞ ((1/(3n+2))−(1/(3n+4))) S = Σ_(n=0) ^∞ (2/((3n+2)(3n+4))) S = (2/9)Σ_(n=0) ^∞ (1/((n+(2/3))(n+(4/3)))) S = (2/9).((ψ((4/3))−ψ((2/3)))/((4/3)−(2/3))) (1) • ψ(z+1) = ψ(z) +(1/z) ⇒ ψ((4/3)) = ψ((1/3)) +3 • ψ(1−z) = ψ(z) +πcot(πz) ⇒ ψ((2/3)) = ψ((1/3)) +πcot((π/3)) ψ((2/3)) = ψ((1/3)) +(π/( (√3))) (1) : S = (2/9).(((ψ((1/3))+3)−(ψ((1/3))+(π/( (√3)))))/(2/3)) S = (2/9)×(3/2) (3−(π/( (√3)))) = 1−(π/(3(√3)))

$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{4}}\right) \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{4}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{9}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)\left({n}+\frac{\mathrm{4}}{\mathrm{3}}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{9}}.\frac{\psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}}\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\bullet\:\psi\left({z}+\mathrm{1}\right)\:\:=\:\psi\left({z}\right)\:+\frac{\mathrm{1}}{{z}} \\ $$$$\Rightarrow\:\psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:+\mathrm{3} \\ $$$$ \\ $$$$\bullet\:\psi\left(\mathrm{1}−{z}\right)\:\:=\:\psi\left({z}\right)\:+\pi\mathrm{cot}\left(\pi{z}\right) \\ $$$$\Rightarrow\:\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:+\pi\mathrm{cot}\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$\:\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:+\frac{\pi}{\:\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{9}}.\frac{\left(\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{3}\right)−\left(\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\:\sqrt{\mathrm{3}}}\right)}{\frac{\mathrm{2}}{\mathrm{3}}}\:\: \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{9}}×\frac{\mathrm{3}}{\mathrm{2}}\:\left(\mathrm{3}−\frac{\pi}{\:\sqrt{\mathrm{3}}}\right)\:=\:\mathrm{1}−\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Commented by Tawa11 last updated on 24/Jul/21

$$\mathrm{Great} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply