Question Number 147879 by 0731619 last updated on 24/Jul/21
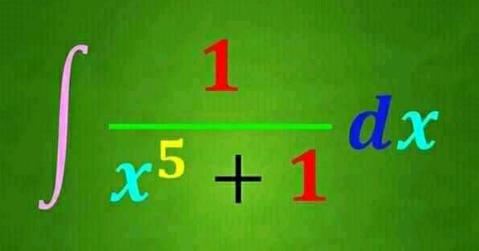
Answered by puissant last updated on 24/Jul/21

$$\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} +\mathrm{1}}\mathrm{dx} \\ $$$$=\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)} \\ $$$$=\int\frac{\frac{\mathrm{1}}{\mathrm{5}}}{\mathrm{x}+\mathrm{1}}\mathrm{dx}+\int\frac{−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{2}}{\mathrm{5}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}+\frac{\mathrm{4}}{\mathrm{5}}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{4}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{4x}^{\mathrm{3}} −\mathrm{8x}^{\mathrm{2}} +\mathrm{12x}−\mathrm{16}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{20}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{5x}^{\mathrm{2}} −\mathrm{14x}+\mathrm{15}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{Q}=\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{5x}^{\mathrm{2}} −\mathrm{14x}+\mathrm{15}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{5x}^{\mathrm{2}} −\mathrm{14x}+\mathrm{15}}{\left(\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{Ax}+\mathrm{B}}{\left(\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\right)}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{Cx}+\mathrm{D}}{\left(\mathrm{x}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\right.}\mathrm{dx} \\ $$$$\mathrm{J}=\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{Ax}+\mathrm{b}}{\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{2}\sqrt{\mathrm{5}}\mathrm{x}+\frac{\mathrm{13}+\mathrm{15}\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\int\frac{\mathrm{2x}+\frac{\mathrm{13}+\mathrm{15}\sqrt{\mathrm{5}}}{\mathrm{10}}}{\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\int\frac{\mathrm{2x}+\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\int\frac{\mathrm{10}\sqrt{\mathrm{5}}+\mathrm{18}}{\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\mid+\frac{\mathrm{10}\sqrt{\mathrm{5}}+\mathrm{18}}{\mathrm{40}\sqrt{\mathrm{5}}}\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\mid+\frac{\mathrm{10}\sqrt{\mathrm{5}}+\mathrm{18}}{\mathrm{40}\sqrt{\mathrm{5}}}×\frac{\mathrm{4}}{\:\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}\mathrm{arctan}\left(\frac{\mathrm{4x}+\sqrt{\mathrm{5}}−\mathrm{1}}{\:\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}\right)+\mathrm{C} \\ $$$$\mathrm{De}\:\mathrm{facon}\:\mathrm{analogue},\:\mathrm{on}\:\mathrm{trouve}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{20}}\int\frac{\mathrm{Cx}+\mathrm{D}}{\mathrm{x}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{10}\sqrt{\mathrm{5}}+\mathrm{18}}{\mathrm{40}\sqrt{\mathrm{5}}}×\frac{\mathrm{4}}{\:\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}\mathrm{arctan}\left(\frac{\mathrm{4x}−\sqrt{\mathrm{5}}−\mathrm{1}}{\:\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}\right)+\mathrm{C} \\ $$$$\mathrm{apres}\:\mathrm{sommation},\:\mathrm{on}\:\mathrm{trouve}: \\ $$$$ \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{20}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\mid \\ $$$$+\frac{\mathrm{10}\sqrt{\mathrm{5}}+\mathrm{18}}{\mathrm{10}\sqrt{\mathrm{5}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}\mathrm{arctan}\left(\frac{\mathrm{4x}+\sqrt{\mathrm{5}}−\mathrm{1}}{\:\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{5}}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{1}\mid \\ $$$$+\frac{\mathrm{10}\sqrt{\mathrm{5}}−\mathrm{18}}{\mathrm{10}\sqrt{\mathrm{5}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}\mathrm{arctan}\left(\frac{\mathrm{4x}−\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)+\mathrm{K}… \\ $$
