Question Number 14797 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
Commented by mrW1 last updated on 05/Jun/17

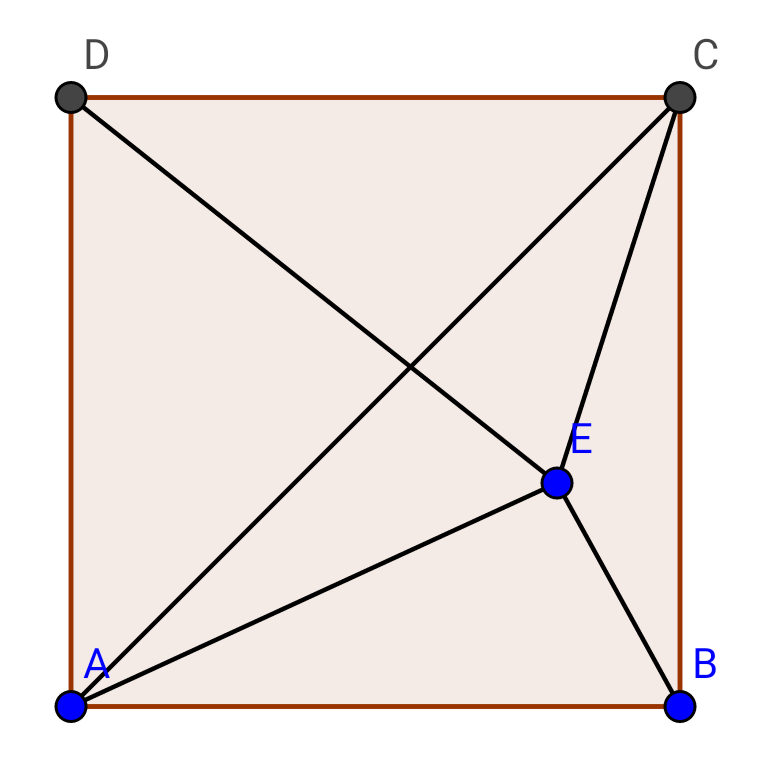
$${we}\:{know}\:{when}\:{the}\:{top}\:{point}\:{of}\:{a} \\ $$$${triangle}\:{is}\:{moved}\:{parallel}\:{to}\:{the}\:{base} \\ $$$${line},\:{the}\:{area}\:{of}\:{the}\:{triangle}\:{remains} \\ $$$${unchanged}. \\ $$$${we}\:{move}\:{the}\:{point}\:{E}\:{in}\:{this}\:{way}\:{such} \\ $$$${that}\:{it}\:{lies}\:{on}\:{the}\:{line}\:{BD}.\: \\ $$$${let}\:{M}={intersection}\:{point}\:{of}\:{AC}\:{and}\:{BD}. \\ $$$${A}_{\Delta{ACE}} =\frac{\mathrm{1}}{\mathrm{2}}×{AC}×{MB} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×{DB}×\left(\frac{{BD}}{\mathrm{2}}−{BE}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\left({DE}+{BE}\right)×\left(\frac{{DE}+{BE}}{\mathrm{2}}−{BE}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{10}+\mathrm{4}\right)×\left(\frac{\mathrm{10}+\mathrm{4}}{\mathrm{2}}−\mathrm{4}\right) \\ $$$$=\mathrm{21} \\ $$$$ \\ $$$${in}\:{general},\:{with}\:{p}={DE}\:{and}\:{q}={BE} \\ $$$${A}_{\Delta{AEC}} =\frac{\left({p}+{q}\right)\left({p}−{q}\right)}{\mathrm{4}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
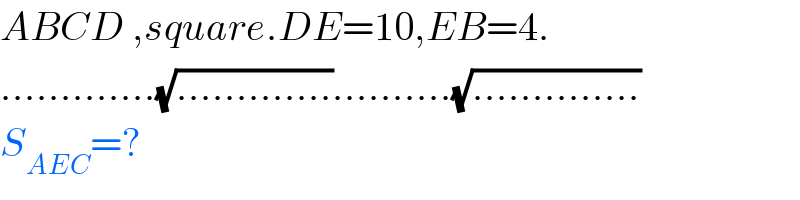
$${ABCD}\:,{square}.{DE}=\mathrm{10},{EB}=\mathrm{4}. \\ $$$$………….\sqrt{………….}……….\sqrt{…………..} \\ $$$${S}_{{AEC}} =? \\ $$
Commented by RasheedSoomro last updated on 04/Jun/17

$$\mathrm{AB}=? \\ $$
Commented by ajfour last updated on 04/Jun/17
Commented by ajfour last updated on 04/Jun/17

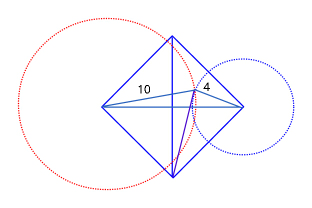
$${C}\:{at}\:{the}\:{top}\:{corner},\:{A}\:{at}\:{the}\: \\ $$$${bottom}.\:{Origin}\:{of}\:{coordinates} \\ $$$${is}\:{center}\:{of}\:{square}.,\:{axes}\:{along} \\ $$$${diagonals}\:{of}\:{square}. \\ $$$${Further}\:{let}\:{side}\:{of}\:{square}=\boldsymbol{{a}}\sqrt{\mathrm{2}} \\ $$$${Equation}\:{of}\:{circles}: \\ $$$$\:\left({x}+{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{100} \\ $$$$\:\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$${subtracting}\:{we}\:{get}\:{x}\:{coordinate} \\ $$$${of}\:{points}\:{of}\:{intersection}: \\ $$$$\:\:\mathrm{4}{ax}\:=\:\mathrm{84}\:\:\:\:\Rightarrow\:\:{ax}=\mathrm{21} \\ $$$${S}_{\bigtriangleup{AEC}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{a}\right){x}=\:{ax}\:=\mathrm{21}\:. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
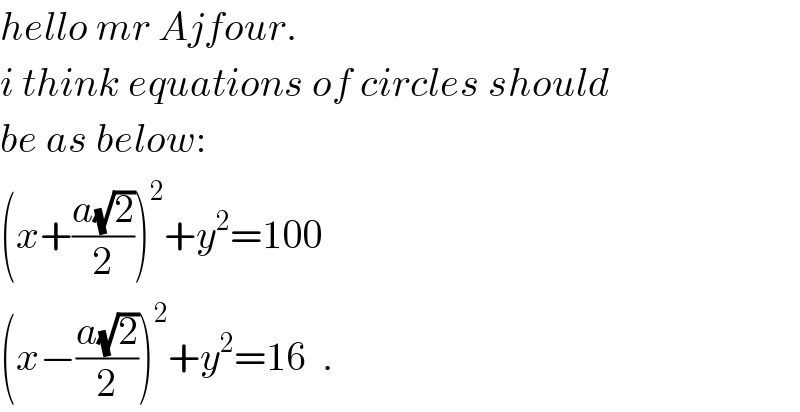
$${hello}\:{mr}\:{Ajfour}. \\ $$$${i}\:{think}\:{equations}\:{of}\:{circles}\:{should} \\ $$$${be}\:{as}\:{below}: \\ $$$$\left({x}+\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{100} \\ $$$$\left({x}−\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16}\:\:. \\ $$
Commented by ajfour last updated on 04/Jun/17
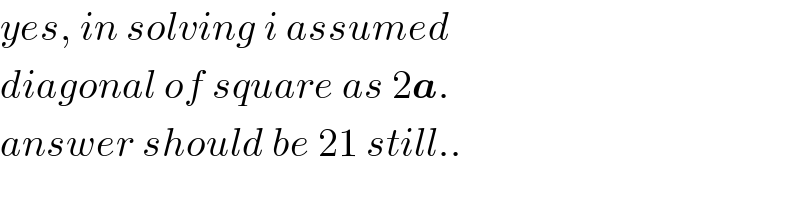
$${yes},\:{in}\:{solving}\:{i}\:{assumed} \\ $$$${diagonal}\:{of}\:{square}\:{as}\:\mathrm{2}\boldsymbol{{a}}.\: \\ $$$${answer}\:{should}\:{be}\:\mathrm{21}\:{still}.. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
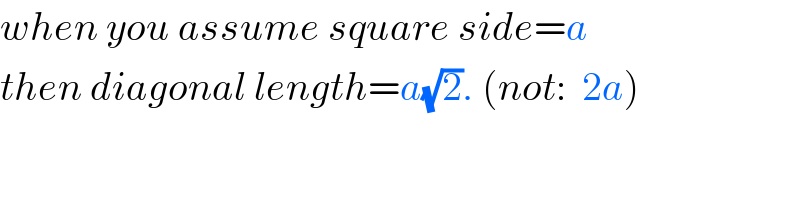
$${when}\:{you}\:{assume}\:{square}\:{side}={a} \\ $$$${then}\:{diagonal}\:{length}={a}\sqrt{\mathrm{2}}.\:\left({not}:\:\:\mathrm{2}{a}\right) \\ $$
Commented by ajfour last updated on 04/Jun/17
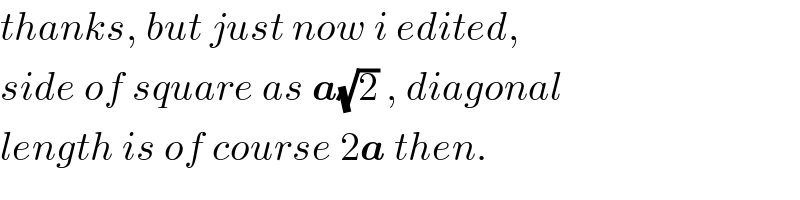
$${thanks},\:{but}\:{just}\:{now}\:{i}\:{edited}, \\ $$$${side}\:{of}\:{square}\:{as}\:\boldsymbol{{a}}\sqrt{\mathrm{2}}\:,\:{diagonal} \\ $$$${length}\:{is}\:{of}\:{course}\:\mathrm{2}\boldsymbol{{a}}\:{then}. \\ $$
Commented by mrW1 last updated on 05/Jun/17
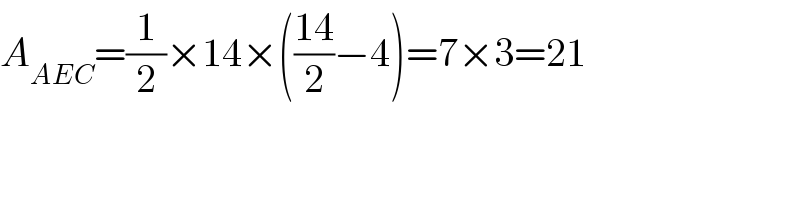
$${A}_{{AEC}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{14}×\left(\frac{\mathrm{14}}{\mathrm{2}}−\mathrm{4}\right)=\mathrm{7}×\mathrm{3}=\mathrm{21} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17
$${so}\:{beautiful}\:{and}\:{nice}! \\ $$$$\:{dear}\:{mrW}\mathrm{1}.{please}\:{show}\:{us}:\:{how}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17
$${nice}\:{and}\:{beautiful}.{thank}\:{a}\:{lot}\:{my}\:{master}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
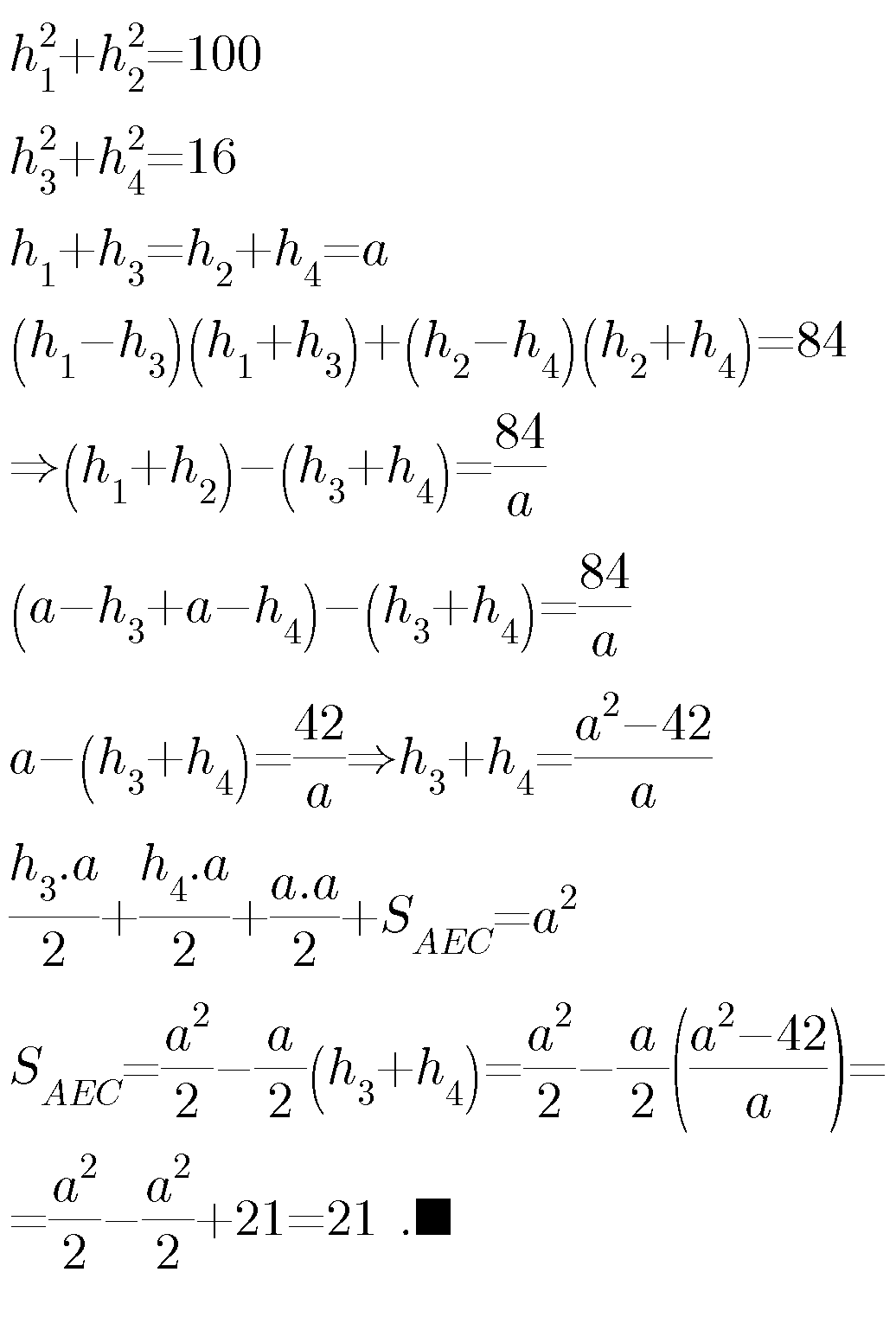
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17
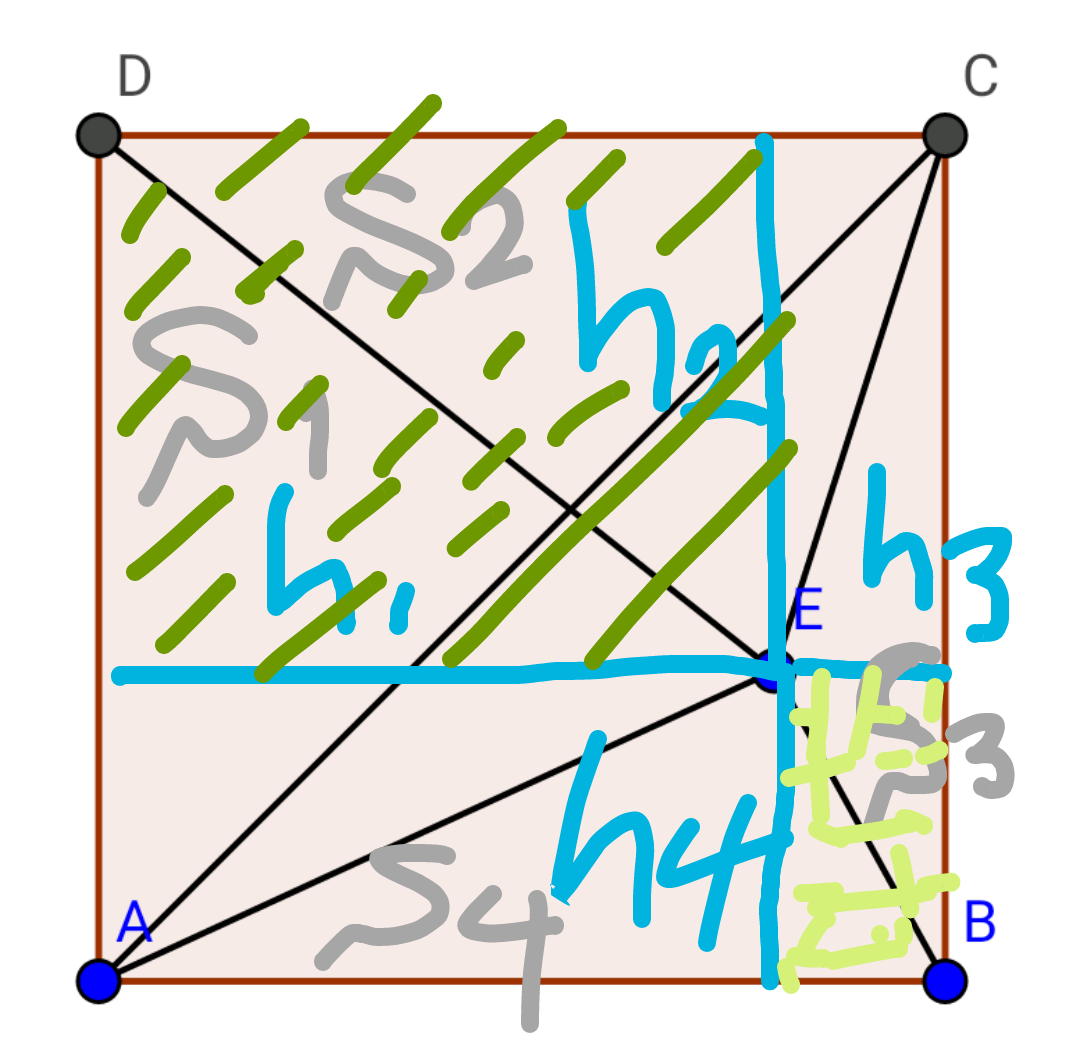
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Jun/17

$${square}\:{sides}=\boldsymbol{{a}} \\ $$
