Question Number 147992 by Sozan last updated on 24/Jul/21
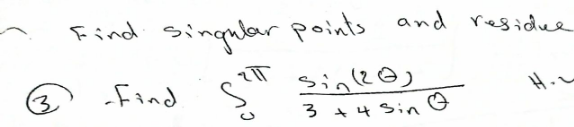
Commented by Sozan last updated on 25/Jul/21
$${who}\:{is}\:{can}\:{solve}\:{this}\:{please}\:? \\ $$
Answered by mathmax by abdo last updated on 25/Jul/21
![Ψ=∫_0 ^(2π) ((sin(2x))/(3+4sinx)) ⇒Ψ=∫_0 ^(2π) ((2sinx.cosx)/(3+4sinx))dx =_(e^(ix) =z) ∫_(∣z∣=1) ((2((z−z^(−1) )/(2i)).((z+z^(−1) )/2))/(3+4((z−z^(−1) )/(2i)))) (dz/(iz)) =∫_(∣z∣=1) ((z^2 −z^(−2) )/(iz(6i+4z−4z^(−1) )))dz =−i∫_(∣z∣=1) ((z^2 −z^(−2) )/(6iz+4z^2 −4))dz =−(i/2)∫_(∣z∣=1) ((z^2 −z^(−2) )/(2z^2 +3iz−2))dz let ϕ(z)=((z^2 −z^(−2) )/(2z^2 +3iz−2)) poles? Δ=−9−4(−4) =16−9=7 ⇒z_1 =((−3i+(√7))/4) z_2 =((−3i−(√7))/4) ∣z_1 ∣−1 =(1/4)(√(9+7))−1 =0 ⇒∣z_1 ∣=1 z_1 z_2 =1 ⇒∣z_2 ∣=1 residus ⇒∫_(∣z∣=1) ϕ(z)dz=2iπ{Res(ϕ,z_1 )+Res(ϕ,z_2 )} but Re(ϕ,z_2 )=−Res(ϕ,z_1 )⇒∫_(∣z∣=1) ϕ(z)dz=0 ⇒Ψ=0 another way Ψ=∫_0 ^π ()dx +∫_π ^(2π) ()dx =_(x=π+α) ∫_0 ^π ((sin2x)/(3+4sinx))dx +∫_0 ^π ((sin(2α))/(3−4sinα))dα =∫_0 ^π sin(2x){(1/(3+4sinx))+(1/(3−4sinx))}dx =∫_0 ^π ((6sin(2x))/(9−16sin^2 x))dx =∫_0 ^π ((6sin(2x))/(9−16(1−cos^2 x)))dx =∫_0 ^π ((6sin(2x))/(16cos^2 x−7))dx =∫_0 ^π ((6sin(2x))/(16.((1+cos(2x))/2)−7))dx =∫_0 ^π ((6sin(2x))/(1+8cos(2x)))dx =(6/(16))∫_0 ^π ((16sin(2x))/(8cos(2x)+1))dx =(3/8)[ln∣8cos(2x)+1∣]_0 ^π =(3/8){ln9−log9}=0](https://www.tinkutara.com/question/Q148006.png)
$$\Psi=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{3}+\mathrm{4sinx}}\:\Rightarrow\Psi=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{2sinx}.\mathrm{cosx}}{\mathrm{3}+\mathrm{4sinx}}\mathrm{dx} \\ $$$$=_{\mathrm{e}^{\mathrm{ix}} \:=\mathrm{z}} \:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2}\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2i}}.\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}}{\mathrm{3}+\mathrm{4}\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2i}}}\:\frac{\mathrm{dz}}{\mathrm{iz}} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}^{−\mathrm{2}} }{\mathrm{iz}\left(\mathrm{6i}+\mathrm{4z}−\mathrm{4z}^{−\mathrm{1}} \right)}\mathrm{dz}\:=−\mathrm{i}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}^{−\mathrm{2}} }{\mathrm{6iz}+\mathrm{4z}^{\mathrm{2}} −\mathrm{4}}\mathrm{dz} \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}^{−\mathrm{2}} }{\mathrm{2z}^{\mathrm{2}} +\mathrm{3iz}−\mathrm{2}}\mathrm{dz}\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}^{−\mathrm{2}} }{\mathrm{2z}^{\mathrm{2}} +\mathrm{3iz}−\mathrm{2}}\:\:\mathrm{poles}? \\ $$$$\Delta=−\mathrm{9}−\mathrm{4}\left(−\mathrm{4}\right)\:=\mathrm{16}−\mathrm{9}=\mathrm{7}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{3i}+\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$$$\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{3i}−\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{9}+\mathrm{7}}−\mathrm{1}\:=\mathrm{0}\:\Rightarrow\mid\mathrm{z}_{\mathrm{1}} \mid=\mathrm{1} \\ $$$$\mathrm{z}_{\mathrm{1}} \mathrm{z}_{\mathrm{2}} =\mathrm{1}\:\Rightarrow\mid\mathrm{z}_{\mathrm{2}} \mid=\mathrm{1}\:\:\mathrm{residus}\:\Rightarrow\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)+\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{2}} \right)\right\} \\ $$$$\mathrm{but}\:\mathrm{Re}\left(\varphi,\mathrm{z}_{\mathrm{2}} \right)=−\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\Rightarrow\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{0}\:\Rightarrow\Psi=\mathrm{0} \\ $$$$\mathrm{another}\:\mathrm{way}\:\Psi=\int_{\mathrm{0}} ^{\pi} \left(\right)\mathrm{dx}\:+\int_{\pi} ^{\mathrm{2}\pi} \left(\right)\mathrm{dx}\:=_{\mathrm{x}=\pi+\alpha} \int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{sin2x}}{\mathrm{3}+\mathrm{4sinx}}\mathrm{dx}\:+\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{sin}\left(\mathrm{2}\alpha\right)}{\mathrm{3}−\mathrm{4sin}\alpha}\mathrm{d}\alpha \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\mathrm{sin}\left(\mathrm{2x}\right)\left\{\frac{\mathrm{1}}{\mathrm{3}+\mathrm{4sinx}}+\frac{\mathrm{1}}{\mathrm{3}−\mathrm{4sinx}}\right\}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{6sin}\left(\mathrm{2x}\right)}{\mathrm{9}−\mathrm{16sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{6sin}\left(\mathrm{2x}\right)}{\mathrm{9}−\mathrm{16}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{6sin}\left(\mathrm{2x}\right)}{\mathrm{16cos}^{\mathrm{2}} \mathrm{x}−\mathrm{7}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{6sin}\left(\mathrm{2x}\right)}{\mathrm{16}.\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}−\mathrm{7}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{6sin}\left(\mathrm{2x}\right)}{\mathrm{1}+\mathrm{8cos}\left(\mathrm{2x}\right)}\mathrm{dx}\:=\frac{\mathrm{6}}{\mathrm{16}}\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{16sin}\left(\mathrm{2x}\right)}{\mathrm{8cos}\left(\mathrm{2x}\right)+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\left[\mathrm{ln}\mid\mathrm{8cos}\left(\mathrm{2x}\right)+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\pi} \:=\frac{\mathrm{3}}{\mathrm{8}}\left\{\mathrm{ln9}−\mathrm{log9}\right\}=\mathrm{0} \\ $$
Commented by tabata last updated on 25/Jul/21
$${msr}\:{mathmax}\:{by}\:{abdo}\:{can}\:{you}\:{help}\:{me}\:{in}\:{question}\:\mathrm{148064}\:{plese} \\ $$
