Question-147999

Question Number 147999 by iloveisrael last updated on 25/Jul/21

Answered by Canebulok last updated on 25/Jul/21

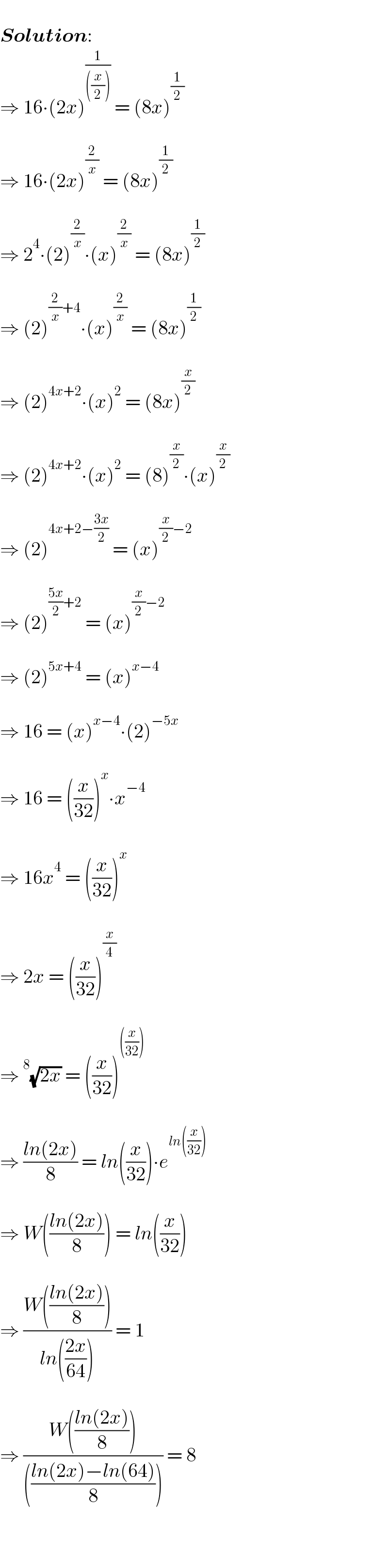
Solution: ⇒ 16∙(2x)^(1/(((x/2)))) = (8x)^(1/2) ⇒ 16∙(2x)^(2/x) = (8x)^(1/2) ⇒ 2^4 ∙(2)^(2/x) ∙(x)^(2/x) = (8x)^(1/2) ⇒ (2)^((2/x)+4) ∙(x)^(2/x) = (8x)^(1/2) ⇒ (2)^(4x+2) ∙(x)^2 = (8x)^(x/2) ⇒ (2)^(4x+2) ∙(x)^2 = (8)^(x/2) ∙(x)^(x/2) ⇒ (2)^(4x+2−((3x)/2)) = (x)^((x/2)−2) ⇒ (2)^(((5x)/2)+2) = (x)^((x/2)−2) ⇒ (2)^(5x+4) = (x)^(x−4) ⇒ 16 = (x)^(x−4) ∙(2)^(−5x) ⇒ 16 = ((x/(32)))^x ∙x^(−4) ⇒ 16x^4 = ((x/(32)))^x ⇒ 2x = ((x/(32)))^(x/4) ⇒^8 (√(2x)) = ((x/(32)))^(((x/(32)))) ⇒ ((ln(2x))/8) = ln((x/(32)))∙e^(ln((x/(32)))) ⇒ W(((ln(2x))/8)) = ln((x/(32))) ⇒ ((W(((ln(2x))/8)))/(ln(((2x)/(64))))) = 1 ⇒ ((W(((ln(2x))/8)))/((((ln(2x)−ln(64))/8)))) = 8

$$\: \\ $$$$\boldsymbol{{Solution}}: \\ $$$$\Rightarrow\:\mathrm{16}\centerdot\left(\mathrm{2}{x}\right)^{\frac{\mathrm{1}}{\left(\frac{{x}}{\mathrm{2}}\right)}} \:=\:\left(\mathrm{8}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\: \\ $$$$\Rightarrow\:\mathrm{16}\centerdot\left(\mathrm{2}{x}\right)^{\frac{\mathrm{2}}{{x}}} \:=\:\left(\mathrm{8}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\: \\ $$$$\Rightarrow\:\mathrm{2}^{\mathrm{4}} \centerdot\left(\mathrm{2}\right)^{\frac{\mathrm{2}}{{x}}} \centerdot\left({x}\right)^{\frac{\mathrm{2}}{{x}}} \:=\:\left(\mathrm{8}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\: \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)^{\frac{\mathrm{2}}{{x}}+\mathrm{4}} \centerdot\left({x}\right)^{\frac{\mathrm{2}}{{x}}} \:=\:\left(\mathrm{8}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\: \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)^{\mathrm{4}{x}+\mathrm{2}} \centerdot\left({x}\right)^{\mathrm{2}} \:=\:\left(\mathrm{8}{x}\right)^{\frac{{x}}{\mathrm{2}}} \\ $$$$\: \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)^{\mathrm{4}{x}+\mathrm{2}} \centerdot\left({x}\right)^{\mathrm{2}} \:=\:\left(\mathrm{8}\right)^{\frac{{x}}{\mathrm{2}}} \centerdot\left({x}\right)^{\frac{{x}}{\mathrm{2}}} \\ $$$$\: \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)^{\mathrm{4}{x}+\mathrm{2}−\frac{\mathrm{3}{x}}{\mathrm{2}}} \:=\:\left({x}\right)^{\frac{{x}}{\mathrm{2}}−\mathrm{2}} \\ $$$$\: \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)^{\frac{\mathrm{5}{x}}{\mathrm{2}}+\mathrm{2}} \:=\:\left({x}\right)^{\frac{{x}}{\mathrm{2}}−\mathrm{2}} \\ $$$$\: \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)^{\mathrm{5}{x}+\mathrm{4}} \:=\:\left({x}\right)^{{x}−\mathrm{4}} \\ $$$$\: \\ $$$$\Rightarrow\:\mathrm{16}\:=\:\left({x}\right)^{{x}−\mathrm{4}} \centerdot\left(\mathrm{2}\right)^{−\mathrm{5}{x}} \\ $$$$\: \\ $$$$\Rightarrow\:\mathrm{16}\:=\:\left(\frac{{x}}{\mathrm{32}}\right)^{{x}} \centerdot{x}^{−\mathrm{4}} \\ $$$$\: \\ $$$$\Rightarrow\:\mathrm{16}{x}^{\mathrm{4}} \:=\:\left(\frac{{x}}{\mathrm{32}}\right)^{{x}} \\ $$$$\: \\ $$$$\Rightarrow\:\mathrm{2}{x}\:=\:\left(\frac{{x}}{\mathrm{32}}\right)^{\frac{{x}}{\mathrm{4}}} \\ $$$$\: \\ $$$$\Rightarrow\:^{\mathrm{8}} \sqrt{\mathrm{2}{x}}\:=\:\left(\frac{{x}}{\mathrm{32}}\right)^{\left(\frac{{x}}{\mathrm{32}}\right)} \\ $$$$\: \\ $$$$\Rightarrow\:\frac{{ln}\left(\mathrm{2}{x}\right)}{\mathrm{8}}\:=\:{ln}\left(\frac{{x}}{\mathrm{32}}\right)\centerdot{e}^{{ln}\left(\frac{{x}}{\mathrm{32}}\right)} \\ $$$$\: \\ $$$$\Rightarrow\:{W}\left(\frac{{ln}\left(\mathrm{2}{x}\right)}{\mathrm{8}}\right)\:=\:{ln}\left(\frac{{x}}{\mathrm{32}}\right) \\ $$$$\: \\ $$$$\Rightarrow\:\frac{{W}\left(\frac{{ln}\left(\mathrm{2}{x}\right)}{\mathrm{8}}\right)}{{ln}\left(\frac{\mathrm{2}{x}}{\mathrm{64}}\right)}\:=\:\mathrm{1} \\ $$$$\: \\ $$$$\Rightarrow\:\frac{{W}\left(\frac{{ln}\left(\mathrm{2}{x}\right)}{\mathrm{8}}\right)}{\left(\frac{{ln}\left(\mathrm{2}{x}\right)−{ln}\left(\mathrm{64}\right)}{\mathrm{8}}\right)}\:=\:\mathrm{8} \\ $$$$\: \\ $$

Commented by iloveisrael last updated on 25/Jul/21

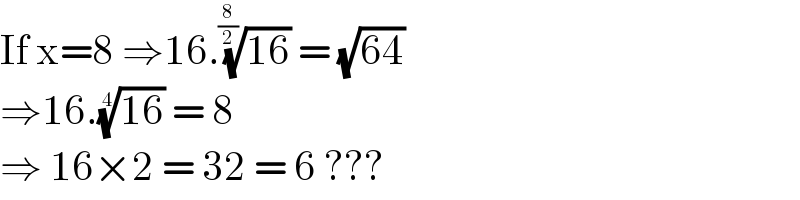
If x=8 ⇒16.((16))^(1/(8/2)) = (√(64)) ⇒16.((16))^(1/4) = 8 ⇒ 16×2 = 32 = 6 ???

$$\mathrm{If}\:\mathrm{x}=\mathrm{8}\:\Rightarrow\mathrm{16}.\sqrt[{\frac{\mathrm{8}}{\mathrm{2}}}]{\mathrm{16}}\:=\:\sqrt{\mathrm{64}} \\ $$$$\Rightarrow\mathrm{16}.\sqrt[{\mathrm{4}}]{\mathrm{16}}\:=\:\mathrm{8} \\ $$$$\Rightarrow\:\mathrm{16}×\mathrm{2}\:=\:\mathrm{32}\:=\:\mathrm{6}\:???\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply