Menu Close

Question-148092

Tinku Tara 0 Comments
Pin




Question Number 148092 by puissant last updated on 25/Jul/21
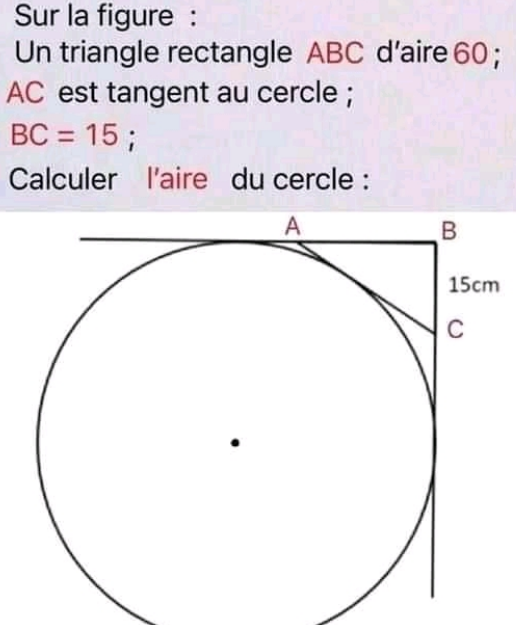
Answered by Olaf_Thorendsen last updated on 25/Jul/21
R est le rayon du cercle. O est le centre du cercle. B ((R),(R) ), C ((R),((R−15)) ) Aire_(ABC) = (1/2)AB×AC ⇒ AB = ((2×Aire_(ABC) )/(AC)) = ((2×60)/(15)) = 8 On en deduit les coordonnees de A et donc du vecteur AC^(→) . A (((R−8)),(R) ), AC^(→) ((8),((−15)) ) Si T est le point de tangence entre la droite (AC) et le cercle, on a necessairement OT^(→) •AC^(→) = 0 car ces deux vecteurs sont perpendiculaires. ⇒ 8x_T −15y_T = 0 (1) La droite (AC) a pour equation : y−y_A = ((y_C −y_A )/(x_C −x_A ))(x−x_A ) y−R = −((15)/8)(x−R+8) T est un point de (AB) et donc : y_T −R = −((15)/8)(x_T −R+8) Avec (1) : y_T = (8/(15))x_T (8/(15))x_T −R = −((15)/8)(x_T −R+8) x_T = ((345)/(289))R−((1800)/(289)) D′ou y_T = (8/(15))x_T = ((184)/(289))R−((960)/(289)) Et puis, T est un point du cercle : x_T ^2 +y_T ^2 = R^2 ( ((345)/(289))R−((1800)/(289)))^2 +(((184)/(289))R−((960)/(289)))^2 = R^2 ((95281)/(57600))R^2 −((6647)/(450))R+((4464)/(225)) = 0 ⇒ R = 3 ou R = 20 La valeur 3 est a rejeter car on cherche une valeur au moins superieure a 15 cm. Et donc : R = 20 cm On peut verifier pour R = 20 : A (((12)),((20)) ), B (((20)),((20)) ), C (((20)),(5) ), T ((((300)/(17))),(((160)/(17))) ) AB = 8 et BC = 15 (AB) : y = −((15)/8)x+((85)/2) On a bien : • BC = 15 • Aire_(ABC) = 60 −((15)/8)(((300)/(17)))+((85)/2) = ((160)/(17)) ⇒ T∈(AB) • (((300)/(17)))^2 +(((160)/(17)))^2 = 400 = 20^2 donc T∈C(O,20) L′aire du cercle est πR^2 , soit 400π
$$\mathrm{R}\:\mathrm{est}\:\mathrm{le}\:\mathrm{rayon}\:\mathrm{du}\:\mathrm{cercle}. \\ $$$$\mathrm{O}\:\mathrm{est}\:\mathrm{le}\:\mathrm{centre}\:\mathrm{du}\:\mathrm{cercle}. \\ $$$$\mathrm{B}\begin{pmatrix}{\mathrm{R}}\\{\mathrm{R}}\end{pmatrix},\:\mathrm{C}\begin{pmatrix}{\mathrm{R}}\\{\mathrm{R}−\mathrm{15}}\end{pmatrix} \\ $$$$\mathrm{Aire}_{\mathrm{ABC}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{AB}×\mathrm{AC} \\ $$$$\Rightarrow\:\mathrm{AB}\:=\:\frac{\mathrm{2}×\mathrm{Aire}_{\mathrm{ABC}} }{\mathrm{AC}}\:=\:\frac{\mathrm{2}×\mathrm{60}}{\mathrm{15}}\:=\:\mathrm{8} \\ $$$$\mathrm{On}\:\mathrm{en}\:\mathrm{deduit}\:\mathrm{les}\:\mathrm{coordonnees}\:\mathrm{de}\:\mathrm{A}\:\mathrm{et} \\ $$$$\mathrm{donc}\:\mathrm{du}\:\mathrm{vecteur}\:\overset{\rightarrow} {\mathrm{AC}}. \\ $$$$\mathrm{A}\begin{pmatrix}{\mathrm{R}−\mathrm{8}}\\{\mathrm{R}}\end{pmatrix},\:\overset{\rightarrow} {\mathrm{AC}}\begin{pmatrix}{\mathrm{8}}\\{−\mathrm{15}}\end{pmatrix} \\ $$$$ \\ $$$$\mathrm{Si}\:\mathrm{T}\:\mathrm{est}\:\mathrm{le}\:\mathrm{point}\:\mathrm{de}\:\mathrm{tangence}\:\mathrm{entre} \\ $$$$\mathrm{la}\:\mathrm{droite}\:\left(\mathrm{AC}\right)\:\mathrm{et}\:\mathrm{le}\:\mathrm{cercle},\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{necessairement}\:\overset{\rightarrow} {\mathrm{OT}}\bullet\overset{\rightarrow} {\mathrm{AC}}\:=\:\mathrm{0}\:\mathrm{car}\:\mathrm{ces} \\ $$$$\mathrm{deux}\:\mathrm{vecteurs}\:\mathrm{sont}\:\mathrm{perpendiculaires}. \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{8}{x}_{\mathrm{T}} −\mathrm{15}{y}_{\mathrm{T}} \:=\:\mathrm{0}\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{La}\:\mathrm{droite}\:\left(\mathrm{AC}\right)\:\mathrm{a}\:\mathrm{pour}\:\mathrm{equation}\:: \\ $$$${y}−{y}_{\mathrm{A}} \:=\:\frac{{y}_{\mathrm{C}} −{y}_{\mathrm{A}} }{{x}_{\mathrm{C}} −{x}_{\mathrm{A}} }\left({x}−{x}_{\mathrm{A}} \right) \\ $$$${y}−\mathrm{R}\:=\:−\frac{\mathrm{15}}{\mathrm{8}}\left({x}−\mathrm{R}+\mathrm{8}\right) \\ $$$$\mathrm{T}\:\mathrm{est}\:\mathrm{un}\:\mathrm{point}\:\mathrm{de}\:\left(\mathrm{AB}\right)\:\mathrm{et}\:\mathrm{donc}\:: \\ $$$${y}_{\mathrm{T}} −\mathrm{R}\:=\:−\frac{\mathrm{15}}{\mathrm{8}}\left({x}_{\mathrm{T}} −\mathrm{R}+\mathrm{8}\right) \\ $$$$\mathrm{Avec}\:\left(\mathrm{1}\right)\::\:{y}_{\mathrm{T}} \:=\:\frac{\mathrm{8}}{\mathrm{15}}{x}_{\mathrm{T}} \\ $$$$\frac{\mathrm{8}}{\mathrm{15}}{x}_{\mathrm{T}} −\mathrm{R}\:=\:−\frac{\mathrm{15}}{\mathrm{8}}\left({x}_{\mathrm{T}} −\mathrm{R}+\mathrm{8}\right) \\ $$$${x}_{\mathrm{T}} \:=\:\frac{\mathrm{345}}{\mathrm{289}}\mathrm{R}−\frac{\mathrm{1800}}{\mathrm{289}} \\ $$$$\mathrm{D}'\mathrm{ou}\:{y}_{\mathrm{T}} \:=\:\frac{\mathrm{8}}{\mathrm{15}}{x}_{\mathrm{T}} \:=\:\frac{\mathrm{184}}{\mathrm{289}}\mathrm{R}−\frac{\mathrm{960}}{\mathrm{289}} \\ $$$$ \\ $$$$\mathrm{Et}\:\mathrm{puis},\:\mathrm{T}\:\mathrm{est}\:\mathrm{un}\:\mathrm{point}\:\mathrm{du}\:\mathrm{cercle}\:: \\ $$$${x}_{\mathrm{T}} ^{\mathrm{2}} +{y}_{\mathrm{T}} ^{\mathrm{2}} \:=\:\mathrm{R}^{\mathrm{2}} \\ $$$$\left(\:\frac{\mathrm{345}}{\mathrm{289}}\mathrm{R}−\frac{\mathrm{1800}}{\mathrm{289}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{184}}{\mathrm{289}}\mathrm{R}−\frac{\mathrm{960}}{\mathrm{289}}\right)^{\mathrm{2}} \:=\:\mathrm{R}^{\mathrm{2}} \\ $$$$\frac{\mathrm{95281}}{\mathrm{57600}}\mathrm{R}^{\mathrm{2}} −\frac{\mathrm{6647}}{\mathrm{450}}\mathrm{R}+\frac{\mathrm{4464}}{\mathrm{225}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{R}\:=\:\mathrm{3}\:\mathrm{ou}\:\mathrm{R}\:=\:\mathrm{20} \\ $$$$\mathrm{La}\:\mathrm{valeur}\:\mathrm{3}\:\mathrm{est}\:\mathrm{a}\:\mathrm{rejeter}\:\mathrm{car}\:\mathrm{on}\:\mathrm{cherche} \\ $$$$\mathrm{une}\:\mathrm{valeur}\:\mathrm{au}\:\mathrm{moins}\:\mathrm{superieure}\:\mathrm{a} \\ $$$$\mathrm{15}\:\mathrm{cm}. \\ $$$$\mathrm{Et}\:\mathrm{donc}\::\:\mathrm{R}\:=\:\mathrm{20}\:\mathrm{cm} \\ $$$$ \\ $$$$\mathrm{On}\:\mathrm{peut}\:\mathrm{verifier}\:\mathrm{pour}\:\mathrm{R}\:=\:\mathrm{20}\:: \\ $$$$\mathrm{A}\begin{pmatrix}{\mathrm{12}}\\{\mathrm{20}}\end{pmatrix},\:\mathrm{B}\begin{pmatrix}{\mathrm{20}}\\{\mathrm{20}}\end{pmatrix},\:\mathrm{C}\begin{pmatrix}{\mathrm{20}}\\{\mathrm{5}}\end{pmatrix},\:\mathrm{T}\begin{pmatrix}{\frac{\mathrm{300}}{\mathrm{17}}}\\{\frac{\mathrm{160}}{\mathrm{17}}}\end{pmatrix} \\ $$$$\mathrm{AB}\:=\:\mathrm{8}\:\mathrm{et}\:\mathrm{BC}\:=\:\mathrm{15} \\ $$$$\left(\mathrm{AB}\right)\::\:{y}\:\:=\:−\frac{\mathrm{15}}{\mathrm{8}}{x}+\frac{\mathrm{85}}{\mathrm{2}} \\ $$$$\mathrm{On}\:\mathrm{a}\:\mathrm{bien}\:: \\ $$$$\bullet\:\mathrm{BC}\:=\:\mathrm{15} \\ $$$$\bullet\:\mathrm{Aire}_{\mathrm{ABC}} \:=\:\mathrm{60} \\ $$$$−\frac{\mathrm{15}}{\mathrm{8}}\left(\frac{\mathrm{300}}{\mathrm{17}}\right)+\frac{\mathrm{85}}{\mathrm{2}}\:=\:\frac{\mathrm{160}}{\mathrm{17}}\:\Rightarrow\:\mathrm{T}\in\left(\mathrm{AB}\right) \\ $$$$\bullet\:\left(\frac{\mathrm{300}}{\mathrm{17}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{160}}{\mathrm{17}}\right)^{\mathrm{2}} =\:\mathrm{400}\:=\:\mathrm{20}^{\mathrm{2}} \\ $$$$\mathrm{donc}\:\mathrm{T}\in\mathscr{C}\left(\mathrm{O},\mathrm{20}\right) \\ $$$$ \\ $$$$\mathrm{L}'\mathrm{aire}\:\mathrm{du}\:\mathrm{cercle}\:\mathrm{est}\:\pi\mathrm{R}^{\mathrm{2}} ,\:\mathrm{soit}\:\mathrm{400}\pi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *