Question-148118

Question Number 148118 by mathdanisur last updated on 25/Jul/21

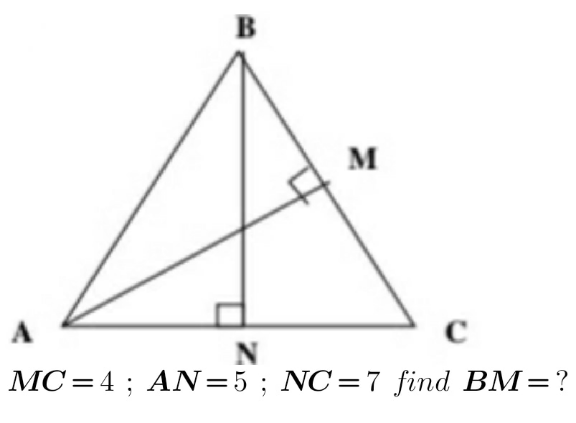
Answered by liberty last updated on 25/Jul/21

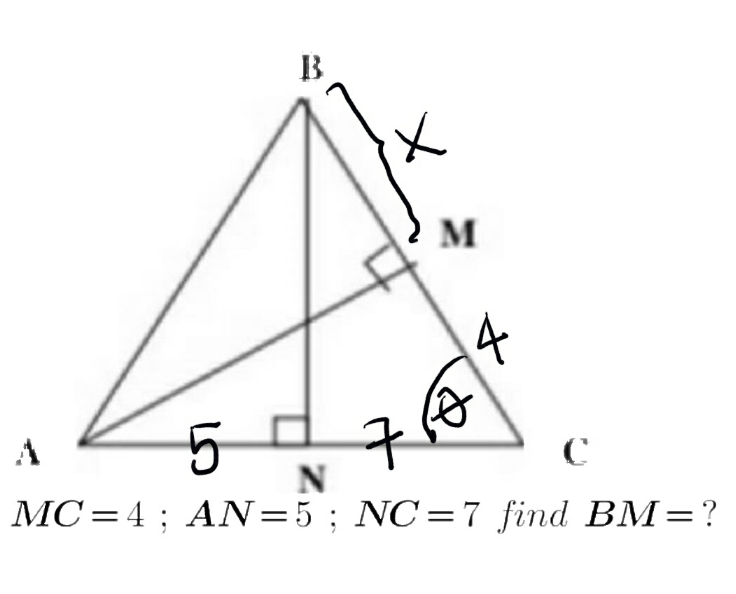
Commented by liberty last updated on 25/Jul/21

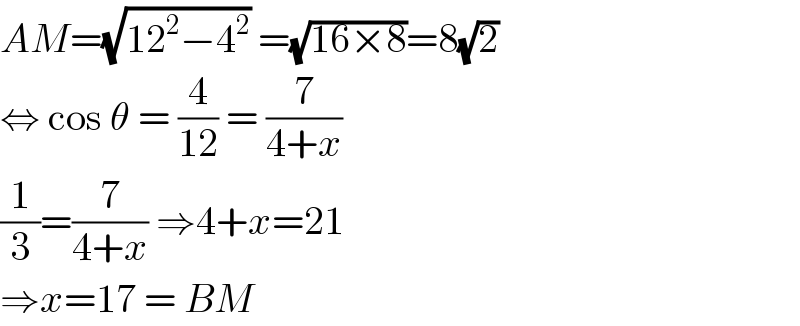
AM=(√(12^2 −4^2 )) =(√(16×8))=8(√2) ⇔ cos θ = (4/(12)) = (7/(4+x)) (1/3)=(7/(4+x)) ⇒4+x=21 ⇒x=17 = BM

$${AM}=\sqrt{\mathrm{12}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }\:=\sqrt{\mathrm{16}×\mathrm{8}}=\mathrm{8}\sqrt{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{cos}\:\theta\:=\:\frac{\mathrm{4}}{\mathrm{12}}\:=\:\frac{\mathrm{7}}{\mathrm{4}+{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{4}+{x}}\:\Rightarrow\mathrm{4}+{x}=\mathrm{21} \\ $$$$\Rightarrow{x}=\mathrm{17}\:=\:{BM} \\ $$

Commented by mathdanisur last updated on 25/Jul/21

$${thank}\:{you}\:{Ser} \\ $$

Answered by Olaf_Thorendsen last updated on 25/Jul/21

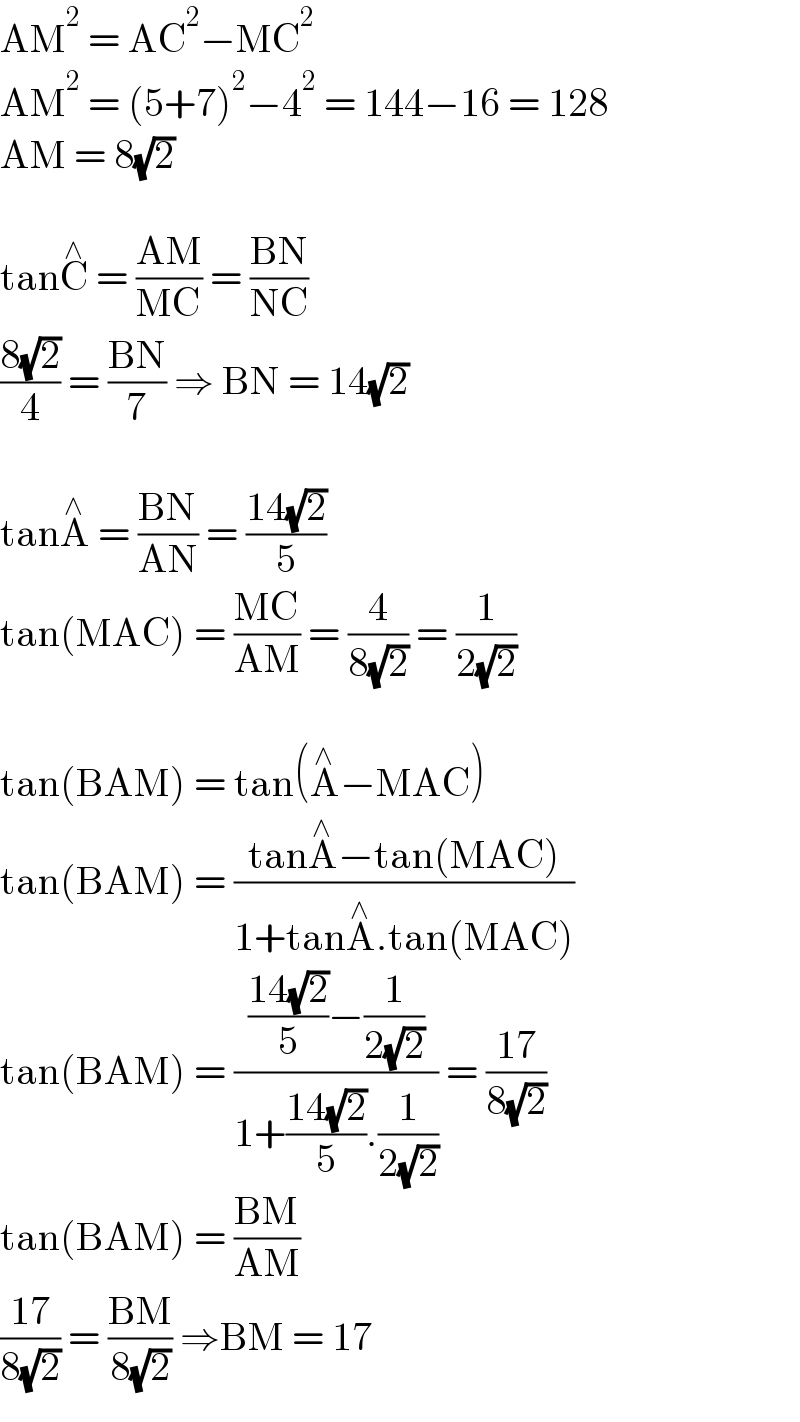
AM^2 = AC^2 −MC^2 AM^2 = (5+7)^2 −4^2 = 144−16 = 128 AM = 8(√2) tanC^∧ = ((AM)/(MC)) = ((BN)/(NC)) ((8(√2))/4) = ((BN)/7) ⇒ BN = 14(√2) tanA^∧ = ((BN)/(AN)) = ((14(√2))/5) tan(MAC) = ((MC)/(AM)) = (4/(8(√2))) = (1/(2(√2))) tan(BAM) = tan(A^∧ −MAC) tan(BAM) = ((tanA^∧ −tan(MAC))/(1+tanA^∧ .tan(MAC))) tan(BAM) = ((((14(√2))/5)−(1/(2(√2))))/(1+((14(√2))/5).(1/(2(√2))))) = ((17)/(8(√2))) tan(BAM) = ((BM)/(AM)) ((17)/(8(√2))) = ((BM)/(8(√2))) ⇒BM = 17

$$\mathrm{AM}^{\mathrm{2}} \:=\:\mathrm{AC}^{\mathrm{2}} −\mathrm{MC}^{\mathrm{2}} \\ $$$$\mathrm{AM}^{\mathrm{2}} \:=\:\left(\mathrm{5}+\mathrm{7}\right)^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} \:=\:\mathrm{144}−\mathrm{16}\:=\:\mathrm{128} \\ $$$$\mathrm{AM}\:=\:\mathrm{8}\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{tan}\overset{\wedge} {\mathrm{C}}\:=\:\frac{\mathrm{AM}}{\mathrm{MC}}\:=\:\frac{\mathrm{BN}}{\mathrm{NC}} \\ $$$$\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{4}}\:=\:\frac{\mathrm{BN}}{\mathrm{7}}\:\Rightarrow\:\mathrm{BN}\:=\:\mathrm{14}\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{tan}\overset{\wedge} {\mathrm{A}}\:=\:\frac{\mathrm{BN}}{\mathrm{AN}}\:=\:\frac{\mathrm{14}\sqrt{\mathrm{2}}}{\mathrm{5}} \\ $$$$\mathrm{tan}\left(\mathrm{MAC}\right)\:=\:\frac{\mathrm{MC}}{\mathrm{AM}}\:=\:\frac{\mathrm{4}}{\mathrm{8}\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$ \\ $$$$\mathrm{tan}\left(\mathrm{BAM}\right)\:=\:\mathrm{tan}\left(\overset{\wedge} {\mathrm{A}}−\mathrm{MAC}\right) \\ $$$$\mathrm{tan}\left(\mathrm{BAM}\right)\:=\:\frac{\mathrm{tan}\overset{\wedge} {\mathrm{A}}−\mathrm{tan}\left(\mathrm{MAC}\right)}{\mathrm{1}+\mathrm{tan}\overset{\wedge} {\mathrm{A}}.\mathrm{tan}\left(\mathrm{MAC}\right)} \\ $$$$\mathrm{tan}\left(\mathrm{BAM}\right)\:=\:\frac{\frac{\mathrm{14}\sqrt{\mathrm{2}}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{1}+\frac{\mathrm{14}\sqrt{\mathrm{2}}}{\mathrm{5}}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}\:=\:\frac{\mathrm{17}}{\mathrm{8}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{tan}\left(\mathrm{BAM}\right)\:=\:\frac{\mathrm{BM}}{\mathrm{AM}} \\ $$$$\frac{\mathrm{17}}{\mathrm{8}\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{BM}}{\mathrm{8}\sqrt{\mathrm{2}}}\:\Rightarrow\mathrm{BM}\:=\:\mathrm{17} \\ $$

Commented by mathdanisur last updated on 25/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply