Menu Close

Question-14816

Tinku Tara 0 Comments
Pin




Question Number 14816 by tawa tawa last updated on 04/Jun/17
Answered by arnabpapu550@gmail.com last updated on 08/Jun/17
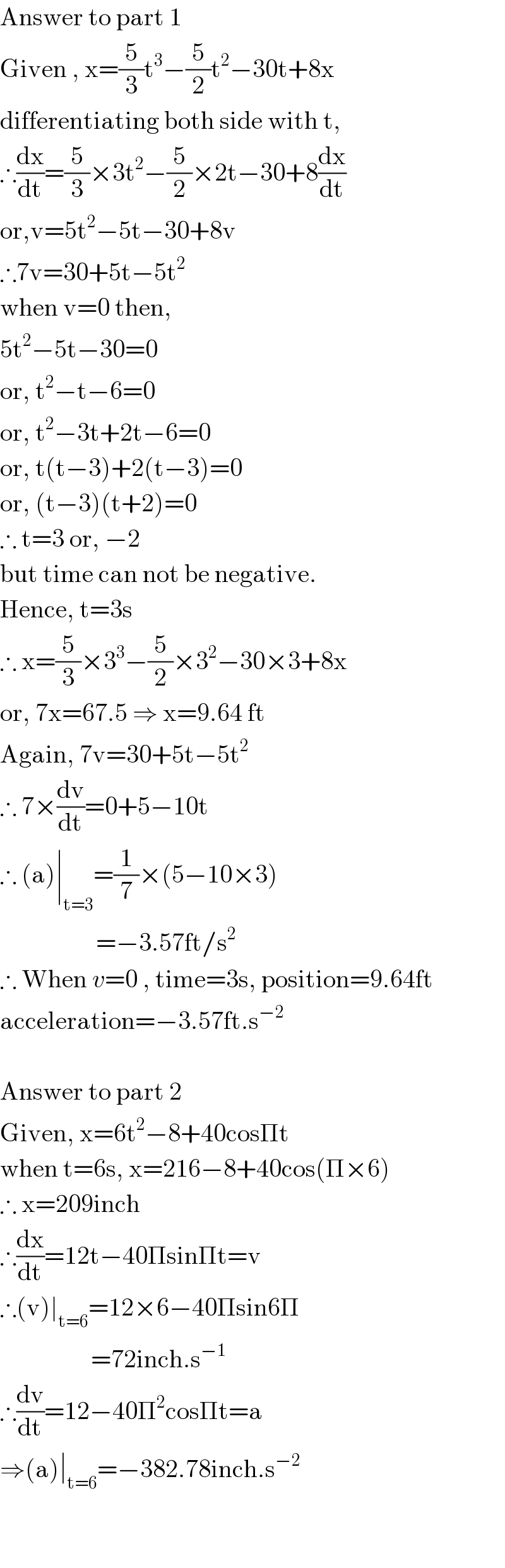
Answer to part 1 Given , x=(5/3)t^3 −(5/2)t^2 −30t+8x differentiating both side with t, ∴(dx/dt)=(5/3)×3t^2 −(5/2)×2t−30+8(dx/dt) or,v=5t^2 −5t−30+8v ∴7v=30+5t−5t^2 when v=0 then, 5t^2 −5t−30=0 or, t^2 −t−6=0 or, t^2 −3t+2t−6=0 or, t(t−3)+2(t−3)=0 or, (t−3)(t+2)=0 ∴ t=3 or, −2 but time can not be negative. Hence, t=3s ∴ x=(5/3)×3^3 −(5/2)×3^2 −30×3+8x or, 7x=67.5 ⇒ x=9.64 ft Again, 7v=30+5t−5t^2 ∴ 7×(dv/dt)=0+5−10t ∴ (a)∣_(t=3) =(1/7)×(5−10×3) =−3.57ft/s^2 ∴ When v=0 , time=3s, position=9.64ft acceleration=−3.57ft.s^(−2) Answer to part 2 Given, x=6t^2 −8+40cosΠt when t=6s, x=216−8+40cos(Π×6) ∴ x=209inch ∴(dx/dt)=12t−40ΠsinΠt=v ∴(v)∣_(t=6) =12×6−40Πsin6Π =72inch.s^(−1) ∴(dv/dt)=12−40Π^2 cosΠt=a ⇒(a)∣_(t=6) =−382.78inch.s^(−2)
$$\mathrm{Answer}\:\mathrm{to}\:\mathrm{part}\:\mathrm{1} \\ $$$$\mathrm{Given}\:,\:\mathrm{x}=\frac{\mathrm{5}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} −\frac{\mathrm{5}}{\mathrm{2}}\mathrm{t}^{\mathrm{2}} −\mathrm{30t}+\mathrm{8x} \\ $$$$\mathrm{differentiating}\:\mathrm{both}\:\mathrm{side}\:\mathrm{with}\:\mathrm{t}, \\ $$$$\therefore\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{5}}{\mathrm{3}}×\mathrm{3t}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}×\mathrm{2t}−\mathrm{30}+\mathrm{8}\frac{\mathrm{dx}}{\mathrm{dt}} \\ $$$$\mathrm{or},\mathrm{v}=\mathrm{5t}^{\mathrm{2}} −\mathrm{5t}−\mathrm{30}+\mathrm{8v} \\ $$$$\therefore\mathrm{7v}=\mathrm{30}+\mathrm{5t}−\mathrm{5t}^{\mathrm{2}} \\ $$$$\mathrm{when}\:\mathrm{v}=\mathrm{0}\:\mathrm{then}, \\ $$$$\mathrm{5t}^{\mathrm{2}} −\mathrm{5t}−\mathrm{30}=\mathrm{0} \\ $$$$\mathrm{or},\:\mathrm{t}^{\mathrm{2}} −\mathrm{t}−\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{or},\:\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{2t}−\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{or},\:\mathrm{t}\left(\mathrm{t}−\mathrm{3}\right)+\mathrm{2}\left(\mathrm{t}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{or},\:\left(\mathrm{t}−\mathrm{3}\right)\left(\mathrm{t}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\therefore\:\mathrm{t}=\mathrm{3}\:\mathrm{or},\:−\mathrm{2} \\ $$$$\mathrm{but}\:\mathrm{time}\:\mathrm{can}\:\mathrm{not}\:\mathrm{be}\:\mathrm{negative}. \\ $$$$\mathrm{Hence},\:\mathrm{t}=\mathrm{3s} \\ $$$$\therefore\:\mathrm{x}=\frac{\mathrm{5}}{\mathrm{3}}×\mathrm{3}^{\mathrm{3}} −\frac{\mathrm{5}}{\mathrm{2}}×\mathrm{3}^{\mathrm{2}} −\mathrm{30}×\mathrm{3}+\mathrm{8x} \\ $$$$\mathrm{or},\:\mathrm{7x}=\mathrm{67}.\mathrm{5}\:\Rightarrow\:\mathrm{x}=\mathrm{9}.\mathrm{64}\:\mathrm{ft} \\ $$$$\mathrm{Again},\:\mathrm{7v}=\mathrm{30}+\mathrm{5t}−\mathrm{5t}^{\mathrm{2}} \\ $$$$\therefore\:\mathrm{7}×\frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{0}+\mathrm{5}−\mathrm{10t} \\ $$$$\therefore\:\left(\mathrm{a}\right)\mid_{\mathrm{t}=\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{7}}×\left(\mathrm{5}−\mathrm{10}×\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{3}.\mathrm{57ft}/\mathrm{s}^{\mathrm{2}} \\ $$$$\therefore\:\mathrm{When}\:{v}=\mathrm{0}\:,\:\mathrm{time}=\mathrm{3s},\:\mathrm{position}=\mathrm{9}.\mathrm{64ft} \\ $$$$\mathrm{acceleration}=−\mathrm{3}.\mathrm{57ft}.\mathrm{s}^{−\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Answer}\:\mathrm{to}\:\mathrm{part}\:\mathrm{2} \\ $$$$\mathrm{Given},\:\mathrm{x}=\mathrm{6t}^{\mathrm{2}} −\mathrm{8}+\mathrm{40cos}\Pi\mathrm{t} \\ $$$$\mathrm{when}\:\mathrm{t}=\mathrm{6s},\:\mathrm{x}=\mathrm{216}−\mathrm{8}+\mathrm{40cos}\left(\Pi×\mathrm{6}\right) \\ $$$$\therefore\:\mathrm{x}=\mathrm{209inch} \\ $$$$\therefore\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{12t}−\mathrm{40}\Pi\mathrm{sin}\Pi\mathrm{t}=\mathrm{v} \\ $$$$\therefore\left(\mathrm{v}\right)\mid_{\mathrm{t}=\mathrm{6}} =\mathrm{12}×\mathrm{6}−\mathrm{40}\Pi\mathrm{sin6}\Pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{72inch}.\mathrm{s}^{−\mathrm{1}} \\ $$$$\therefore\frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{12}−\mathrm{40}\prod^{\mathrm{2}} \mathrm{cos}\Pi\mathrm{t}=\mathrm{a} \\ $$$$\Rightarrow\left(\mathrm{a}\right)\mid_{\mathrm{t}=\mathrm{6}} =−\mathrm{382}.\mathrm{78inch}.\mathrm{s}^{−\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *