Question Number 148171 by ajfour last updated on 25/Jul/21

Commented by ajfour last updated on 25/Jul/21

$${This}\:{bird}\:{caged}\:{inside}\:{this}\: \\ $$$${tetrahedron}\:{has}\:{to}\:{start}\:{from} \\ $$$${origin},\:{touch}\:{each}\:{centroidal} \\ $$$${points}\:{of}\:{the}\:{faces}\:{and}\:{get} \\ $$$${back}.\:{If}\:{tetrahedron}\:{is}\:{regular} \\ $$$${with}\:{edge}\:{a},\:{find}\:{minimum}\: \\ $$$${distance}\:{of}\:{the}\:{journey}. \\ $$$$\left({worm}\:{holes}\:{not}\:{allowed}\:\::\right) \\ $$
Answered by mr W last updated on 25/Jul/21

Commented by mr W last updated on 25/Jul/21
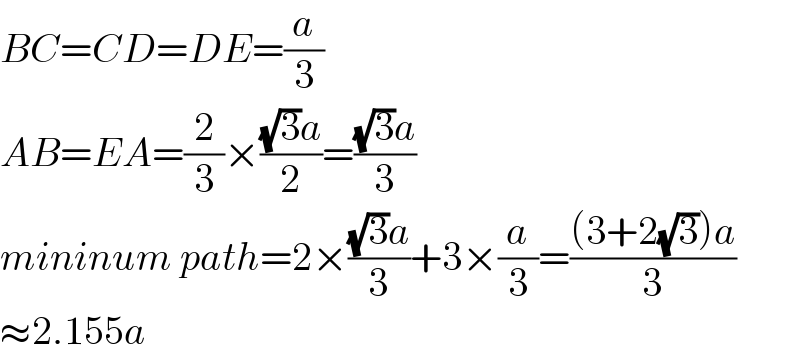
$${BC}={CD}={DE}=\frac{{a}}{\mathrm{3}} \\ $$$${AB}={EA}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}} \\ $$$${mininum}\:{path}=\mathrm{2}×\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}}+\mathrm{3}×\frac{{a}}{\mathrm{3}}=\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\right){a}}{\mathrm{3}} \\ $$$$\approx\mathrm{2}.\mathrm{155}{a} \\ $$
Commented by ajfour last updated on 25/Jul/21

$${I}\:{had}\:{not}\:{thought}\:{it}\:{wd}\:{b}\:{that} \\ $$$${easy},\:{thank}\:{you}\:{sir},\:{correct} \\ $$$${n}\:{great}\:{image}. \\ $$
