Question-148222

Question Number 148222 by BHOOPENDRA last updated on 26/Jul/21

Answered by iloveisrael last updated on 26/Jul/21

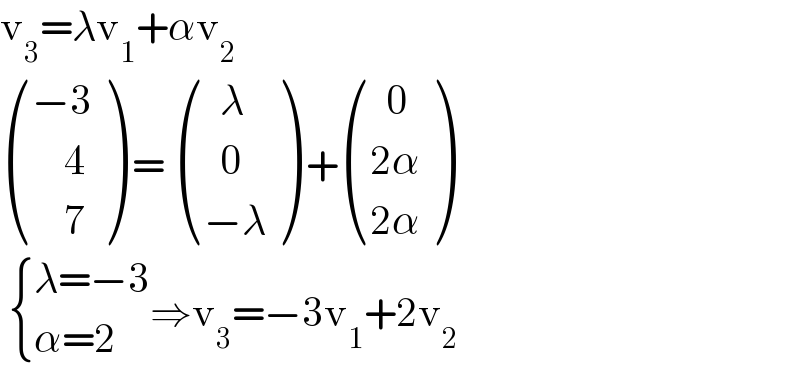
v_3 =λv_1 +αv_2 (((−3)),(( 4)),(( 7)) ) = ((( λ)),(( 0)),((−λ)) ) + ((( 0)),((2α)),((2α)) ) { ((λ=−3)),((α=2)) :}⇒v_3 =−3v_1 +2v_2

$$\mathrm{v}_{\mathrm{3}} =\lambda\mathrm{v}_{\mathrm{1}} +\alpha\mathrm{v}_{\mathrm{2}} \\ $$$$\begin{pmatrix}{−\mathrm{3}}\\{\:\:\:\:\mathrm{4}}\\{\:\:\:\:\mathrm{7}}\end{pmatrix}\:=\:\begin{pmatrix}{\:\:\lambda}\\{\:\:\mathrm{0}}\\{−\lambda}\end{pmatrix}\:+\begin{pmatrix}{\:\:\mathrm{0}}\\{\mathrm{2}\alpha}\\{\mathrm{2}\alpha}\end{pmatrix} \\ $$$$\:\begin{cases}{\lambda=−\mathrm{3}}\\{\alpha=\mathrm{2}}\end{cases}\Rightarrow\mathrm{v}_{\mathrm{3}} =−\mathrm{3v}_{\mathrm{1}} +\mathrm{2v}_{\mathrm{2}} \\ $$

Commented by BHOOPENDRA last updated on 26/Jul/21

$${what}\:{about}\:{the}\:{other}\:{two}\:{sir}\:? \\ $$

Answered by Olaf_Thorendsen last updated on 26/Jul/21

(ii) Let v = ((x),(y),(z) ) ∈ W then ∃(α,β,γ)∈R^3 \ v = αv_1 +αv_2 +γv_3 v = αv_1 +βv_2 +γ(−3v_1 +2v_2 ) v = (α−3γ)v_1 +(β+2γ)v_2 Let a = α−3γ and b = β+2γ then ∃(a,b)∈R^2 \ v = av_1 +bv_2 That proves that (v_1 ,v_2 ) generates W. (iii) We solve the equation λv_1 +μv_2 = 0_W (1) ⇔ λ ((1),(0),((−1)) )+μ ((0),(2),(2) ) = ((0),(0),(0) ) ⇔ (λ,μ) = (0,0) We canno′t find (λ,μ)∈R^2 −{(0,0)} such that (1) is true. That proves that v_1 and v_2 are linearly independent.

$$ \\ $$$$\left(\mathrm{ii}\right) \\ $$$$\mathrm{Let}\:{v}\:=\:\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}\:\in\:{W} \\ $$$$\mathrm{then}\:\exists\left(\alpha,\beta,\gamma\right)\in\mathbb{R}^{\mathrm{3}} \:\backslash\:{v}\:=\:\alpha{v}_{\mathrm{1}} +\alpha{v}_{\mathrm{2}} +\gamma{v}_{\mathrm{3}} \\ $$$${v}\:=\:\alpha{v}_{\mathrm{1}} +\beta{v}_{\mathrm{2}} +\gamma\left(−\mathrm{3}{v}_{\mathrm{1}} +\mathrm{2}{v}_{\mathrm{2}} \right) \\ $$$${v}\:=\:\left(\alpha−\mathrm{3}\gamma\right){v}_{\mathrm{1}} +\left(\beta+\mathrm{2}\gamma\right){v}_{\mathrm{2}} \\ $$$$\mathrm{Let}\:{a}\:=\:\alpha−\mathrm{3}\gamma\:\mathrm{and}\:{b}\:=\:\beta+\mathrm{2}\gamma \\ $$$$\mathrm{then}\:\exists\left({a},{b}\right)\in\mathbb{R}^{\mathrm{2}} \:\backslash\:{v}\:=\:{av}_{\mathrm{1}} +{bv}_{\mathrm{2}} \\ $$$$\mathrm{That}\:\mathrm{proves}\:\mathrm{that}\:\left({v}_{\mathrm{1}} ,{v}_{\mathrm{2}} \right)\:\mathrm{generates}\:{W}. \\ $$$$ \\ $$$$\left(\mathrm{iii}\right) \\ $$$$\mathrm{We}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\lambda{v}_{\mathrm{1}} +\mu{v}_{\mathrm{2}} \:=\:\mathrm{0}_{{W}} \:\:\:\left(\mathrm{1}\right) \\ $$$$\Leftrightarrow\:\lambda\begin{pmatrix}{\mathrm{1}}\\{\mathrm{0}}\\{−\mathrm{1}}\end{pmatrix}+\mu\begin{pmatrix}{\mathrm{0}}\\{\mathrm{2}}\\{\mathrm{2}}\end{pmatrix}\:\:=\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\Leftrightarrow\:\left(\lambda,\mu\right)\:=\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{We}\:\mathrm{canno}'\mathrm{t}\:\mathrm{find}\:\left(\lambda,\mu\right)\in\mathbb{R}^{\mathrm{2}} −\left\{\left(\mathrm{0},\mathrm{0}\right)\right\} \\ $$$$\mathrm{such}\:\mathrm{that}\:\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{true}. \\ $$$$\mathrm{That}\:\mathrm{proves}\:\mathrm{that}\:{v}_{\mathrm{1}} \:\mathrm{and}\:{v}_{\mathrm{2}} \:\mathrm{are} \\ $$$$\mathrm{linearly}\:\mathrm{independent}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply