Question Number 148229 by iloveisrael last updated on 26/Jul/21
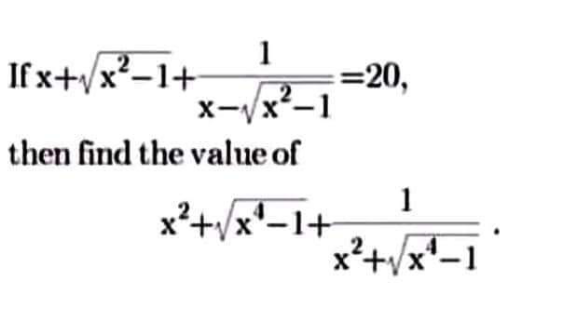
Commented by nimnim last updated on 26/Jul/21
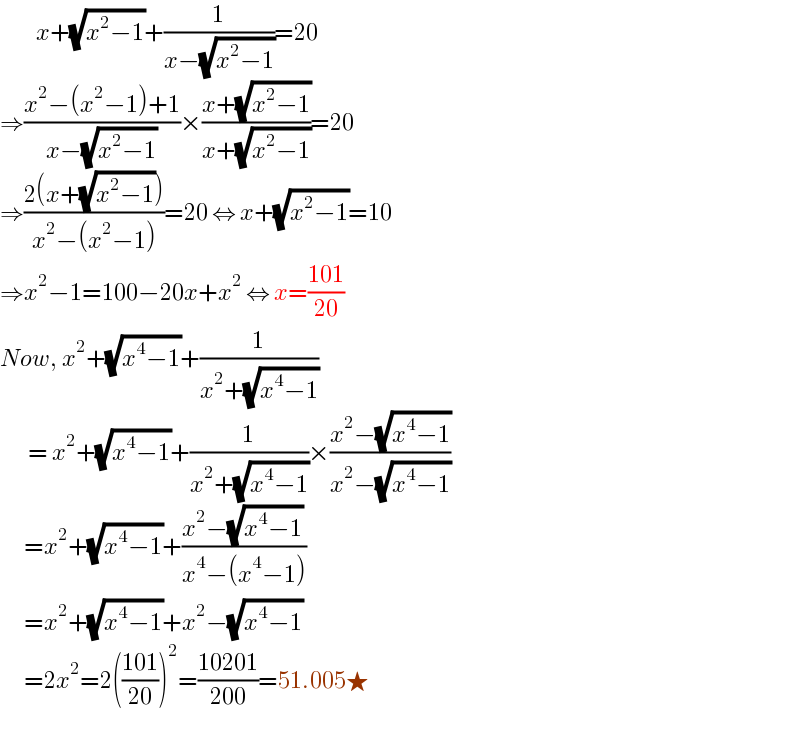
$$\:\:\:\:\:\:\:\:\:{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{20} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{2}} −\left({x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{1}}{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}×\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{20} \\ $$$$\Rightarrow\frac{\mathrm{2}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)}{{x}^{\mathrm{2}} −\left({x}^{\mathrm{2}} −\mathrm{1}\right)}=\mathrm{20}\:\Leftrightarrow\:{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}=\mathrm{10} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{100}−\mathrm{20}{x}+{x}^{\mathrm{2}} \:\Leftrightarrow\:{x}=\frac{\mathrm{101}}{\mathrm{20}} \\ $$$${Now},\:{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:=\:{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}×\frac{{x}^{\mathrm{2}} −\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}{{x}^{\mathrm{2}} −\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}} \\ $$$$\:\:\:\:\:\:={x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}+\frac{{x}^{\mathrm{2}} −\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}{{x}^{\mathrm{4}} −\left({x}^{\mathrm{4}} −\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:={x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}+{x}^{\mathrm{2}} −\sqrt{{x}^{\mathrm{4}} −\mathrm{1}} \\ $$$$\:\:\:\:\:\:=\mathrm{2}{x}^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{101}}{\mathrm{20}}\right)^{\mathrm{2}} =\frac{\mathrm{10201}}{\mathrm{200}}=\mathrm{51}.\mathrm{005}\bigstar \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by EDWIN88 last updated on 26/Jul/21
![(1)(x+(√(x^2 −1)))(x−(√(x^2 −1)))+1=20(x−(√(x^2 −1))) ⇒2 = 20(x−(√(x^2 −1))) ⇒(√(x^2 −1)) = x−(1/(10)) ⇒x^2 −1= x^2 −(x/5)+(1/(100)) ⇒(x/5)=((101)/(100)) , x=((101)/(20)) (2)x^2 +(√(x^4 −1)) +(1/(x^2 +(√(x^4 −1)))) =? (•) x^2 −1+(√((x^2 −1)(x^2 +1)))+1 = (x+1)(x−1)+(√((x+1)(x−1)(x^2 +1)))+1 = (((121)/(20)))(((81)/(20)))+(√((((121)/(20)))(((81)/(20)))(((101^2 +20^2 )/(20^2 )))))+1 = ((9801)/(400))+((99(√(10601)))/(400)) +1 =((99(√(10601))+10201)/(400)) so x^2 +(√(x^4 −1))+(1/(x^2 +(√(x^4 −1)))) = ((99(√(10601))+10201)/(400)) +((400)/( 99(√(10601))+10201)) [ love Jew ]](https://www.tinkutara.com/question/Q148230.png)
$$\left(\mathrm{1}\right)\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\left({x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)+\mathrm{1}=\mathrm{20}\left({x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\Rightarrow\mathrm{2}\:=\:\mathrm{20}\left({x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:{x}−\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{1}=\:{x}^{\mathrm{2}} −\frac{{x}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{100}} \\ $$$$\Rightarrow\frac{{x}}{\mathrm{5}}=\frac{\mathrm{101}}{\mathrm{100}}\:,\:{x}=\frac{\mathrm{101}}{\mathrm{20}} \\ $$$$\left(\mathrm{2}\right){x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}\:=? \\ $$$$\left(\bullet\right)\:{x}^{\mathrm{2}} −\mathrm{1}+\sqrt{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}+\mathrm{1} \\ $$$$\:=\:\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)+\sqrt{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}+\mathrm{1} \\ $$$$=\:\left(\frac{\mathrm{121}}{\mathrm{20}}\right)\left(\frac{\mathrm{81}}{\mathrm{20}}\right)+\sqrt{\left(\frac{\mathrm{121}}{\mathrm{20}}\right)\left(\frac{\mathrm{81}}{\mathrm{20}}\right)\left(\frac{\mathrm{101}^{\mathrm{2}} +\mathrm{20}^{\mathrm{2}} }{\mathrm{20}^{\mathrm{2}} }\right)}+\mathrm{1} \\ $$$$=\:\frac{\mathrm{9801}}{\mathrm{400}}+\frac{\mathrm{99}\sqrt{\mathrm{10601}}}{\mathrm{400}}\:+\mathrm{1} \\ $$$$=\frac{\mathrm{99}\sqrt{\mathrm{10601}}+\mathrm{10201}}{\mathrm{400}} \\ $$$${so}\:{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{4}} −\mathrm{1}}}\:= \\ $$$$\:\frac{\mathrm{99}\sqrt{\mathrm{10601}}+\mathrm{10201}}{\mathrm{400}}\:+\frac{\mathrm{400}}{\:\mathrm{99}\sqrt{\mathrm{10601}}+\mathrm{10201}} \\ $$$$\:\:\:\:\:\:\:\left[\:{love}\:{Jew}\:\right]\: \\ $$
