Menu Close

Question-148257

Tinku Tara 0 Comments
Pin




Question Number 148257 by liberty last updated on 26/Jul/21
Answered by Olaf_Thorendsen last updated on 26/Jul/21
(2^x −4)^3 +(4^x −2)^3 = (4^x +2^x −6)^3 Let u = 2^x (u−4)^3 +(u^2 −2)^3 = (u^2 +u−6)^3 (u−4)^3 +(u^2 −2)^3 = [(u^2 −2)+(u−4)]^3 0 = 3(u^2 −2)^2 (u−4)+3(u^2 −2)(u−4)^2 (u^2 −2)(u−4)(u^2 −2+u−4) = 0 (u+(√2))(u−(√2))(u−4)(u+3)(u−2) = 0 u = ±(√2), 4,−3, 2 −(√2), −3 impossible because u = 2^x >0 u = (√2), 2, 4 ⇒ x = (1/2), 1, 2 S = {(1/2), 1, 2}
$$\left(\mathrm{2}^{{x}} −\mathrm{4}\right)^{\mathrm{3}} +\left(\mathrm{4}^{{x}} −\mathrm{2}\right)^{\mathrm{3}} \:=\:\left(\mathrm{4}^{{x}} +\mathrm{2}^{{x}} −\mathrm{6}\right)^{\mathrm{3}} \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{2}^{{x}} \\ $$$$\left({u}−\mathrm{4}\right)^{\mathrm{3}} +\left({u}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{3}} \:=\:\left({u}^{\mathrm{2}} +{u}−\mathrm{6}\right)^{\mathrm{3}} \\ $$$$\left({u}−\mathrm{4}\right)^{\mathrm{3}} +\left({u}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{3}} \:=\:\left[\left({u}^{\mathrm{2}} −\mathrm{2}\right)+\left({u}−\mathrm{4}\right)\right]^{\mathrm{3}} \\ $$$$\mathrm{0}\:=\:\mathrm{3}\left({u}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \left({u}−\mathrm{4}\right)+\mathrm{3}\left({u}^{\mathrm{2}} −\mathrm{2}\right)\left({u}−\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\left({u}^{\mathrm{2}} −\mathrm{2}\right)\left({u}−\mathrm{4}\right)\left({u}^{\mathrm{2}} −\mathrm{2}+{u}−\mathrm{4}\right)\:=\:\mathrm{0} \\ $$$$\left({u}+\sqrt{\mathrm{2}}\right)\left({u}−\sqrt{\mathrm{2}}\right)\left({u}−\mathrm{4}\right)\left({u}+\mathrm{3}\right)\left({u}−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$${u}\:=\:\pm\sqrt{\mathrm{2}},\:\mathrm{4},−\mathrm{3},\:\mathrm{2} \\ $$$$ \\ $$$$−\sqrt{\mathrm{2}},\:−\mathrm{3}\:\mathrm{impossible}\:\mathrm{because}\:{u}\:=\:\mathrm{2}^{{x}} >\mathrm{0} \\ $$$${u}\:=\:\sqrt{\mathrm{2}},\:\mathrm{2},\:\mathrm{4}\:\Rightarrow\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{1},\:\mathrm{2} \\ $$$$\mathcal{S}\:=\:\left\{\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{1},\:\mathrm{2}\right\} \\ $$
Answered by Rasheed.Sindhi last updated on 26/Jul/21
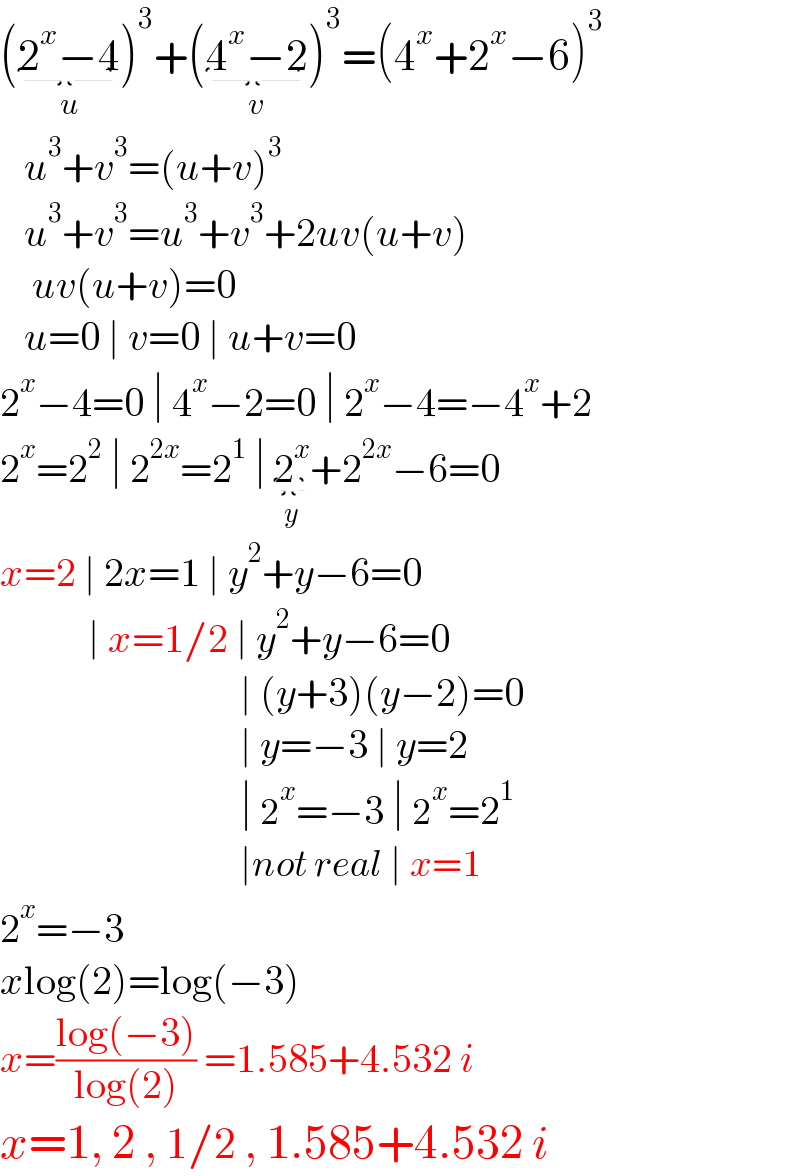
(2^x −4_(u) )^3 +(4^x −2_(v) )^3 =(4^x +2^x −6)^3 u^3 +v^3 =(u+v)^3 u^3 +v^3 =u^3 +v^3 +2uv(u+v) uv(u+v)=0 u=0 ∣ v=0 ∣ u+v=0 2^x −4=0 ∣ 4^x −2=0 ∣ 2^x −4=−4^x +2 2^x =2^2 ∣ 2^(2x) =2^1 ∣ 2^x _(y) +2^(2x) −6=0 x=2 ∣ 2x=1 ∣ y^2 +y−6=0 ∣ x=1/2 ∣ y^2 +y−6=0 ∣ (y+3)(y−2)=0 ∣ y=−3 ∣ y=2 ∣ 2^x =−3 ∣ 2^x =2^1 ∣not real ∣ x=1 2^x =−3 xlog(2)=log(−3) x=((log(−3))/(log(2))) =1.585+4.532 i x=1, 2 , 1/2 , 1.585+4.532 i
$$\left(\underset{{u}} {\underbrace{\mathrm{2}^{{x}} −\mathrm{4}}}\right)^{\mathrm{3}} +\left(\underset{{v}} {\underbrace{\mathrm{4}^{{x}} −\mathrm{2}}}\right)^{\mathrm{3}} =\left(\mathrm{4}^{{x}} +\mathrm{2}^{{x}} −\mathrm{6}\right)^{\mathrm{3}} \\ $$$$\:\:\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =\left({u}+{v}\right)^{\mathrm{3}} \\ $$$$\:\:\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} ={u}^{\mathrm{3}} +{v}^{\mathrm{3}} +\mathrm{2}{uv}\left({u}+{v}\right) \\ $$$$\:\:\:\:{uv}\left({u}+{v}\right)=\mathrm{0} \\ $$$$\:\:\:{u}=\mathrm{0}\:\mid\:{v}=\mathrm{0}\:\mid\:{u}+{v}=\mathrm{0} \\ $$$$\mathrm{2}^{{x}} −\mathrm{4}=\mathrm{0}\:\mid\:\mathrm{4}^{{x}} −\mathrm{2}=\mathrm{0}\:\mid\:\mathrm{2}^{{x}} −\mathrm{4}=−\mathrm{4}^{{x}} +\mathrm{2} \\ $$$$\mathrm{2}^{{x}} =\mathrm{2}^{\mathrm{2}} \:\mid\:\mathrm{2}^{\mathrm{2}{x}} =\mathrm{2}^{\mathrm{1}} \:\mid\:\underset{{y}} {\underbrace{\mathrm{2}^{{x}} }}+\mathrm{2}^{\mathrm{2}{x}} −\mathrm{6}=\mathrm{0} \\ $$$${x}=\mathrm{2}\:\mid\:\mathrm{2}{x}=\mathrm{1}\:\mid\:{y}^{\mathrm{2}} +{y}−\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mid\:{x}=\mathrm{1}/\mathrm{2}\:\mid\:{y}^{\mathrm{2}} +{y}−\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\left({y}+\mathrm{3}\right)\left({y}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:{y}=−\mathrm{3}\:\mid\:{y}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\mathrm{2}^{{x}} =−\mathrm{3}\:\mid\:\mathrm{2}^{{x}} =\mathrm{2}^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{not}\:{real}\:\mid\:{x}=\mathrm{1} \\ $$$$\mathrm{2}^{{x}} =−\mathrm{3} \\ $$$${x}\mathrm{log}\left(\mathrm{2}\right)=\mathrm{log}\left(−\mathrm{3}\right) \\ $$$${x}=\frac{\mathrm{log}\left(−\mathrm{3}\right)}{\mathrm{log}\left(\mathrm{2}\right)}\:=\mathrm{1}.\mathrm{585}+\mathrm{4}.\mathrm{532}\:{i}\: \\ $$$${x}=\mathrm{1},\:\mathrm{2}\:,\:\mathrm{1}/\mathrm{2}\:,\:\mathrm{1}.\mathrm{585}+\mathrm{4}.\mathrm{532}\:{i} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *