Question Number 148268 by mathdanisur last updated on 26/Jul/21
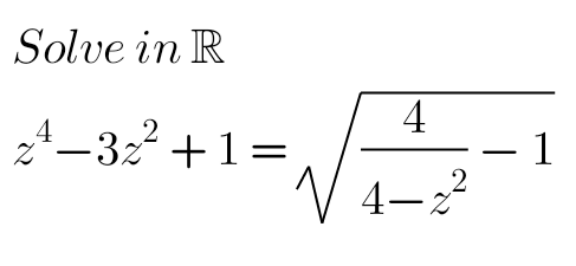
Answered by Olaf_Thorendsen last updated on 26/Jul/21

$${z}^{\mathrm{4}} −\mathrm{3}{z}^{\mathrm{2}} +\mathrm{1}\:=\:\sqrt{\frac{\mathrm{4}}{\mathrm{4}−{z}^{\mathrm{2}} }−\mathrm{1}}\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Let}\:{w}\:=\:{z}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\::\:{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{1}\:=\:\sqrt{\frac{\mathrm{4}}{\mathrm{4}−{w}}−\mathrm{1}} \\ $$$$\Rightarrow\:\left(\ast\right)\:{w}^{\mathrm{4}} −\mathrm{6}{w}^{\mathrm{3}} +\mathrm{11}{w}^{\mathrm{2}} −\mathrm{6}{w}+\mathrm{1}\:=\:\frac{{w}}{\mathrm{4}−{w}} \\ $$$${w}^{\mathrm{5}} −\mathrm{10}{w}^{\mathrm{4}} +\mathrm{35}{w}^{\mathrm{3}} −\mathrm{50}{w}^{\mathrm{2}} +\mathrm{26}{w}−\mathrm{4}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\left({w}^{\mathrm{5}} −\mathrm{2}{w}^{\mathrm{4}} \right)−\mathrm{8}\left({w}^{\mathrm{4}} −\mathrm{2}{w}^{\mathrm{3}} \right)+\mathrm{19}\left({w}^{\mathrm{3}} −\mathrm{2}{w}^{\mathrm{2}} \right) \\ $$$$−\mathrm{12}\left({w}^{\mathrm{2}} −\mathrm{2}{w}\right)+\mathrm{2}\left({w}−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$${w}^{\mathrm{4}} \left({w}−\mathrm{2}\right)−\mathrm{8}{w}^{\mathrm{3}} \left({w}−\mathrm{2}\right)+\mathrm{19}{w}^{\mathrm{2}} \left({w}−\mathrm{2}\right) \\ $$$$−\mathrm{12}{w}\left({w}−\mathrm{2}\right)+\mathrm{2}\left({w}−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$$\left({w}−\mathrm{2}\right)\left({w}^{\mathrm{4}} −\mathrm{8}{w}^{\mathrm{3}} +\mathrm{19}{w}^{\mathrm{2}} −\mathrm{12}{w}+\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$\left({w}−\mathrm{2}\right)\left({w}^{\mathrm{2}} +{pw}+\mathrm{2}\right)\left({w}^{\mathrm{2}} +{qw}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{By}\:\mathrm{identification}\:{p}\:=\:{q}\:=\:−\mathrm{4} \\ $$$$\left({w}−\mathrm{2}\right)\left({w}^{\mathrm{2}} −\mathrm{4}{w}+\mathrm{2}\right)\left({w}^{\mathrm{2}} −\mathrm{4}{w}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\left({w}−\mathrm{2}\right)\left({w}−\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\right)\left({w}−\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left({w}−\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\right)\left({w}−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\right)\:=\:\mathrm{0}\right. \\ $$$$ \\ $$$${w}\:=\:\mathrm{2},\:{w}\:=\:\mathrm{2}\pm\sqrt{\mathrm{2}},\:{w}\:=\:\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\Rightarrow{z}\:=\:\pm\sqrt{\mathrm{2}},\:{z}\:=\:\pm\sqrt{\mathrm{2}\pm\sqrt{\mathrm{2}}},\:{z}\:=\:\pm\sqrt{\mathrm{2}\pm\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$\left(\ast\right)\:\mathrm{Because}\:\mathrm{of}\:\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{verify} \\ $$$$\mathrm{each}\:\mathrm{solution}.\:\pm\sqrt{\mathrm{2}}\:\mathrm{and}\:\pm\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\: \\ $$$$\mathrm{are}\:\mathrm{not}\:\mathrm{good}. \\ $$$$ \\ $$$$\mathcal{S}\:=\:\left\{\pm\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}},\:\pm\sqrt{\mathrm{2}\pm\sqrt{\mathrm{3}}}\right\} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 26/Jul/21
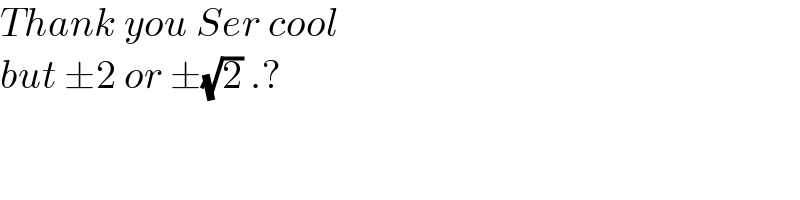
$${Thank}\:{you}\:{Ser}\:{cool} \\ $$$${but}\:\pm\mathrm{2}\:{or}\:\pm\sqrt{\mathrm{2}}\:.? \\ $$
Commented by Olaf_Thorendsen last updated on 26/Jul/21

$$\mathrm{I}\:\mathrm{corrected}\:\mathrm{sir}. \\ $$
Commented by mathdanisur last updated on 26/Jul/21

$${Thanks}\:{Ser} \\ $$
