Question Number 148321 by mathdanisur last updated on 27/Jul/21

Answered by dumitrel last updated on 27/Jul/21
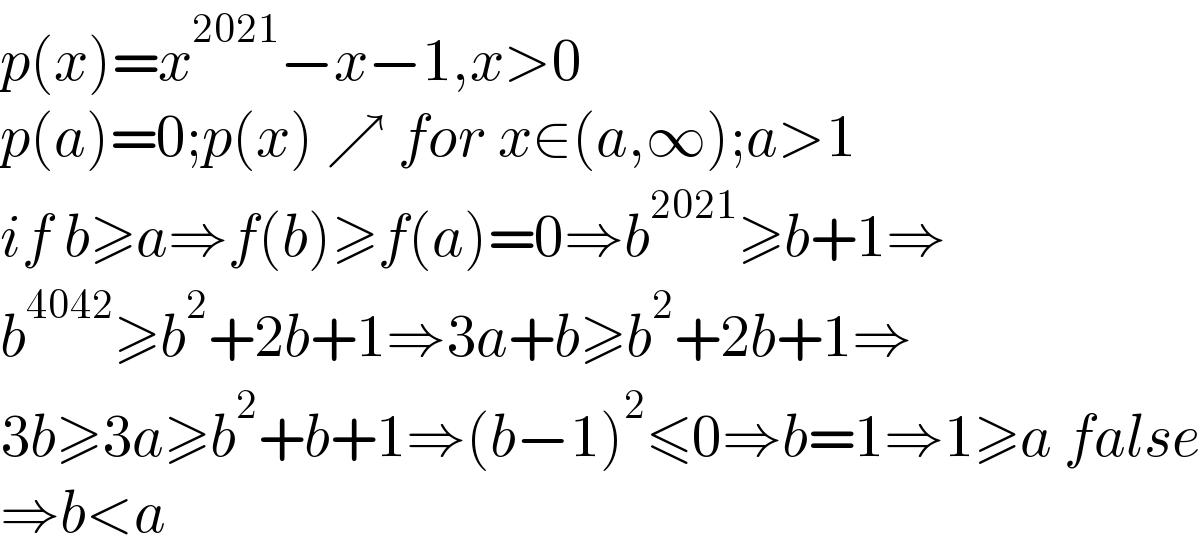
$${p}\left({x}\right)={x}^{\mathrm{2021}} −{x}−\mathrm{1},{x}>\mathrm{0} \\ $$$${p}\left({a}\right)=\mathrm{0};{p}\left({x}\right)\:\nearrow\:{for}\:{x}\in\left({a},\infty\right);{a}>\mathrm{1} \\ $$$${if}\:{b}\geqslant{a}\Rightarrow{f}\left({b}\right)\geqslant{f}\left({a}\right)=\mathrm{0}\Rightarrow{b}^{\mathrm{2021}} \geqslant{b}+\mathrm{1}\Rightarrow \\ $$$${b}^{\mathrm{4042}} \geqslant{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}\Rightarrow\mathrm{3}{a}+{b}\geqslant{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}\Rightarrow \\ $$$$\mathrm{3}{b}\geqslant\mathrm{3}{a}\geqslant{b}^{\mathrm{2}} +{b}+\mathrm{1}\Rightarrow\left({b}−\mathrm{1}\right)^{\mathrm{2}} \leqslant\mathrm{0}\Rightarrow{b}=\mathrm{1}\Rightarrow\mathrm{1}\geqslant{a}\:{false} \\ $$$$\Rightarrow{b}<{a} \\ $$
Commented by mathdanisur last updated on 27/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
