Question-148364

Question Number 148364 by mathdanisur last updated on 27/Jul/21

Commented by dumitrel last updated on 27/Jul/21

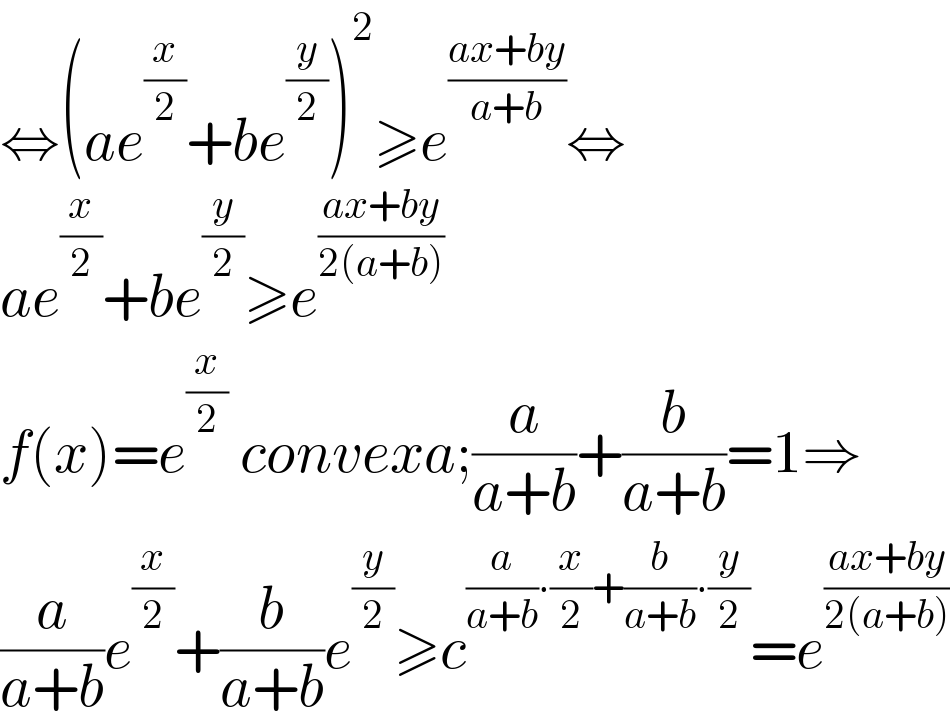
⇔(ae^(x/2) +be^(y/2) )^2 ≥e^((ax+by)/(a+b)) ⇔ ae^(x/2) +be^(y/2) ≥e^((ax+by)/(2(a+b))) f(x)=e^(x/2) convexa;(a/(a+b))+(b/(a+b))=1⇒ (a/(a+b))e^(x/2) +(b/(a+b))e^(y/2) ≥c^((a/(a+b))∙(x/2)+(b/(a+b))∙(y/2)) =e^((ax+by)/(2(a+b)))

$$\Leftrightarrow\left({ae}^{\frac{{x}}{\mathrm{2}}} +{be}^{\frac{{y}}{\mathrm{2}}} \right)^{\mathrm{2}} \geqslant{e}^{\frac{{ax}+{by}}{{a}+{b}}} \Leftrightarrow \\ $$$${ae}^{\frac{{x}}{\mathrm{2}}} +{be}^{\frac{{y}}{\mathrm{2}}} \geqslant{e}^{\frac{{ax}+{by}}{\mathrm{2}\left({a}+{b}\right)}} \\ $$$${f}\left({x}\right)={e}^{\frac{{x}}{\mathrm{2}}} \:{convexa};\frac{{a}}{{a}+{b}}+\frac{{b}}{{a}+{b}}=\mathrm{1}\Rightarrow \\ $$$$\frac{{a}}{{a}+{b}}{e}^{\frac{{x}}{\mathrm{2}}} +\frac{{b}}{{a}+{b}}{e}^{\frac{{y}}{\mathrm{2}}} \geqslant{c}^{\frac{{a}}{{a}+{b}}\centerdot\frac{{x}}{\mathrm{2}}+\frac{{b}}{{a}+{b}}\centerdot\frac{{y}}{\mathrm{2}}} ={e}^{\frac{{ax}+{by}}{\mathrm{2}\left({a}+{b}\right)}} \\ $$

Commented by mathdanisur last updated on 27/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$

Facebook Tweet Pin

Question-148364

Leave a Reply Cancel reply