Question-148427

Question Number 148427 by Rustambek last updated on 27/Jul/21

Answered by Ar Brandon last updated on 27/Jul/21

S=2+Σ_(k=2) ^(2020) (((k+1)k)/((1/(k!))+(1/((k−1)!)))) =2+Σ_(k=2) ^(2020) ((k(k+1)!)/(1+k))=2+Σ_(k=2) ^(2020) k(k!) =2+Σ_(k=2) ^(2020) [(k+1)−1](k!)=2+Σ_(k=2) ^(2020) [(k+1)!−k!] =2+[(3!−2!)+(4!−3!)+∙∙∙(2021!−2020!)] =2021!

$$\mathrm{S}=\mathrm{2}+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{2020}} {\sum}}\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{k}}{\frac{\mathrm{1}}{\mathrm{k}!}+\frac{\mathrm{1}}{\left(\mathrm{k}−\mathrm{1}\right)!}} \\ $$$$\:\:\:=\mathrm{2}+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{2020}} {\sum}}\frac{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)!}{\mathrm{1}+\mathrm{k}}=\mathrm{2}+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{2020}} {\sum}}\mathrm{k}\left(\mathrm{k}!\right) \\ $$$$\:\:\:=\mathrm{2}+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{2020}} {\sum}}\left[\left(\mathrm{k}+\mathrm{1}\right)−\mathrm{1}\right]\left(\mathrm{k}!\right)=\mathrm{2}+\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{2020}} {\sum}}\left[\left(\mathrm{k}+\mathrm{1}\right)!−\mathrm{k}!\right] \\ $$$$\:\:\:=\mathrm{2}+\left[\left(\mathrm{3}!−\mathrm{2}!\right)+\left(\mathrm{4}!−\mathrm{3}!\right)+\centerdot\centerdot\centerdot\left(\mathrm{2021}!−\mathrm{2020}!\right)\right] \\ $$$$\:\:\:=\mathrm{2021}! \\ $$

Commented by Rustambek last updated on 27/Jul/21

$$? \\ $$

Answered by Olaf_Thorendsen last updated on 27/Jul/21

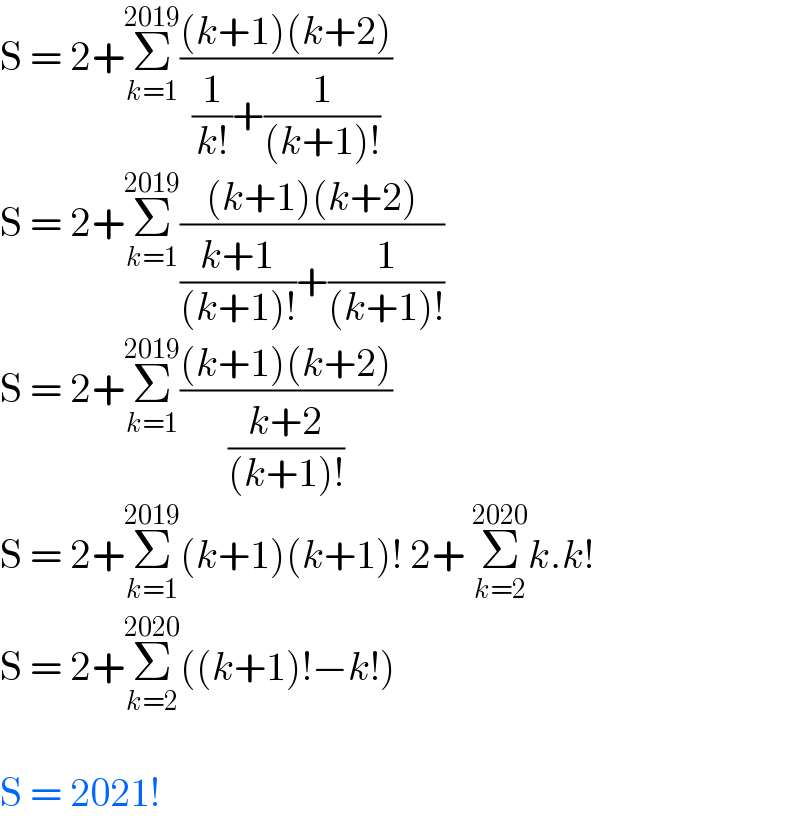
S = 2+Σ_(k=1) ^(2019) (((k+1)(k+2))/((1/(k!))+(1/((k+1)!)))) S = 2+Σ_(k=1) ^(2019) (((k+1)(k+2))/(((k+1)/((k+1)!))+(1/((k+1)!)))) S = 2+Σ_(k=1) ^(2019) (((k+1)(k+2))/((k+2)/((k+1)!))) S = 2+Σ_(k=1) ^(2019) (k+1)(k+1)! 2+ Σ_(k=2) ^(2020) k.k! S = 2+Σ_(k=2) ^(2020) ((k+1)!−k!) S = 2021!

$$\mathrm{S}\:=\:\mathrm{2}+\underset{{k}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}{\frac{\mathrm{1}}{{k}!}+\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!}} \\ $$$$\mathrm{S}\:=\:\mathrm{2}+\underset{{k}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}{\frac{{k}+\mathrm{1}}{\left({k}+\mathrm{1}\right)!}+\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!}} \\ $$$$\mathrm{S}\:=\:\mathrm{2}+\underset{{k}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}{\frac{{k}+\mathrm{2}}{\left({k}+\mathrm{1}\right)!}} \\ $$$$\mathrm{S}\:=\:\mathrm{2}+\underset{{k}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{1}\right)!\:\mathrm{2}+\:\underset{{k}=\mathrm{2}} {\overset{\mathrm{2020}} {\sum}}{k}.{k}! \\ $$$$\mathrm{S}\:=\:\mathrm{2}+\underset{{k}=\mathrm{2}} {\overset{\mathrm{2020}} {\sum}}\left(\left({k}+\mathrm{1}\right)!−{k}!\right) \\ $$$$ \\ $$$$\mathrm{S}\:=\:\mathrm{2021}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply