Question Number 148467 by bramlexs22 last updated on 28/Jul/21
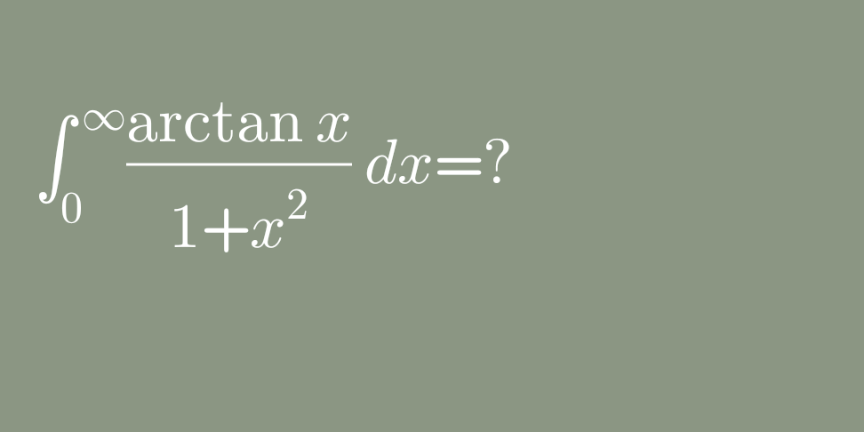
Answered by puissant last updated on 28/Jul/21
![x=tan(t)⇒dx=1+tan^2 (t)dt 0≤x≤∞ ⇒ 0≤t≤(π/2) ⇒I=∫_0 ^(π/2) ((arctan(tan(t)))/(1+tan^2 (t)))(1+tan^2 (t))dt =∫_0 ^(π/2) tdt = (1/2)[t^2 ]_0 ^(π/2) = (1/2)×(π^2 /4)=(π^2 /8) ⇒I = (π^2 /8)....Trivial.](https://www.tinkutara.com/question/Q148471.png)
$$\mathrm{x}=\mathrm{tan}\left(\mathrm{t}\right)\Rightarrow\mathrm{dx}=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{0}\leqslant\mathrm{x}\leqslant\infty\:\Rightarrow\:\mathrm{0}\leqslant\mathrm{t}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{arctan}\left(\mathrm{tan}\left(\mathrm{t}\right)\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{t}\right)}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{tdt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{t}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi^{\mathrm{2}} }{\mathrm{4}}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}}….\mathrm{Trivial}. \\ $$
Answered by Ar Brandon last updated on 28/Jul/21
![I=∫_0 ^∞ ((arctanx)/(1+x^2 ))dx =∫_0 ^(π/2) udu=[(u^2 /2)]_0 ^(π/2) =(π^2 /8)](https://www.tinkutara.com/question/Q148484.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{arctanx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{udu}=\left[\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by Ar Brandon last updated on 28/Jul/21
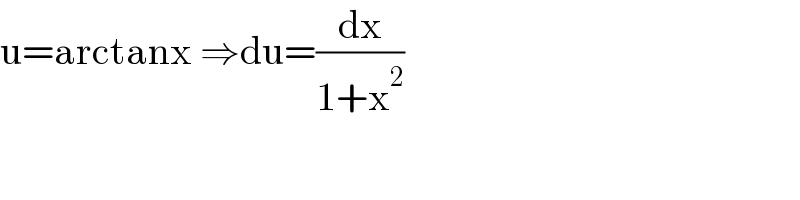
$$\mathrm{u}=\mathrm{arctanx}\:\Rightarrow\mathrm{du}=\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$
