Question Number 148532 by cherokeesay last updated on 28/Jul/21
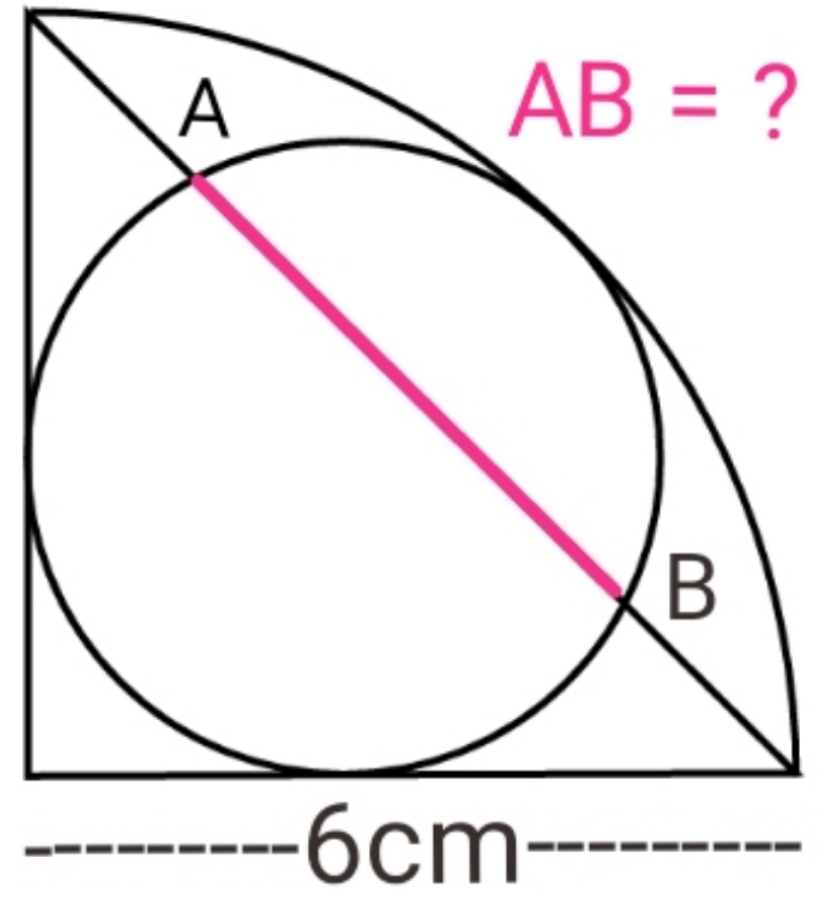
Answered by mr W last updated on 29/Jul/21
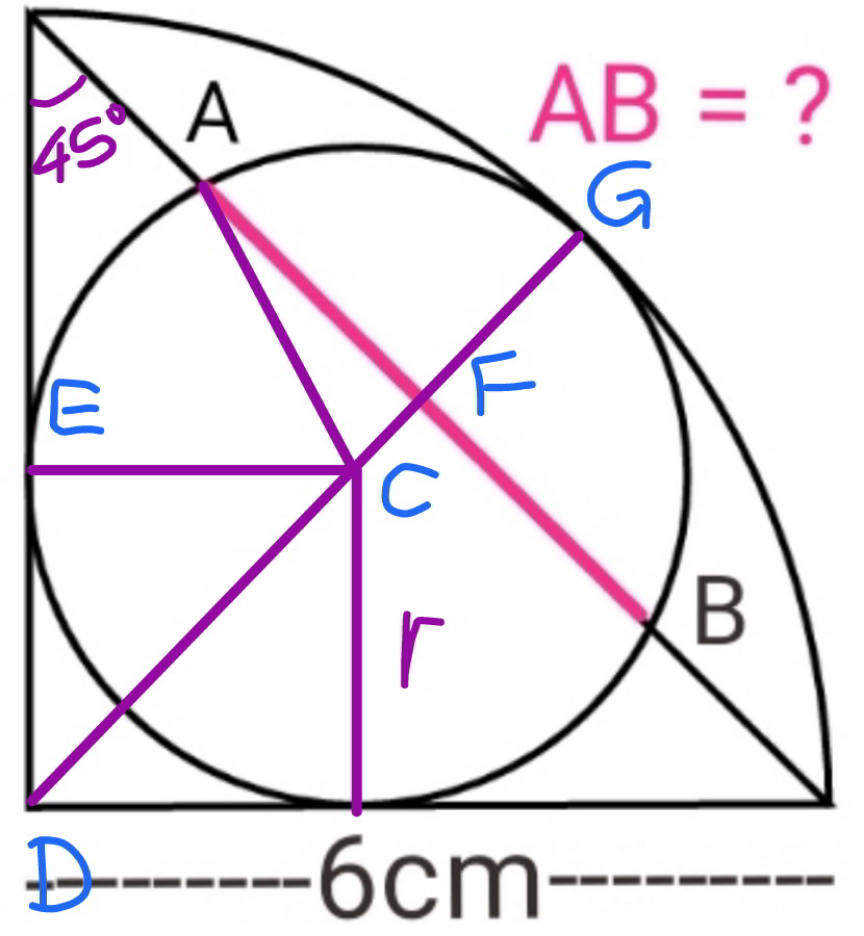
Commented by mr W last updated on 29/Jul/21
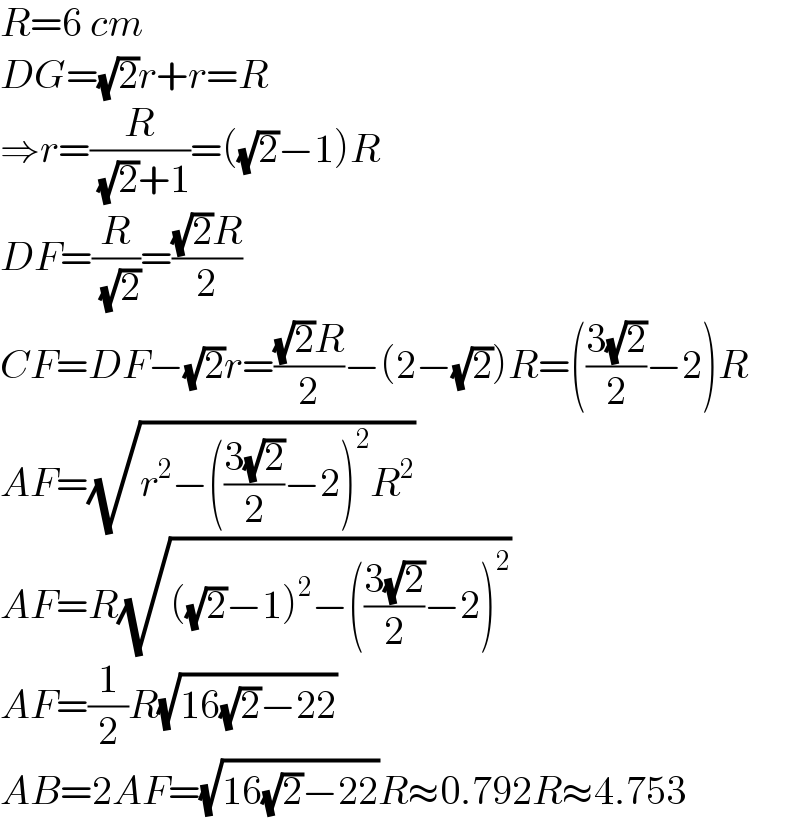
$${R}=\mathrm{6}\:{cm} \\ $$$${DG}=\sqrt{\mathrm{2}}{r}+{r}={R} \\ $$$$\Rightarrow{r}=\frac{{R}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right){R} \\ $$$${DF}=\frac{{R}}{\:\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}{R}}{\mathrm{2}} \\ $$$${CF}={DF}−\sqrt{\mathrm{2}}{r}=\frac{\sqrt{\mathrm{2}}{R}}{\mathrm{2}}−\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){R}=\left(\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}−\mathrm{2}\right){R} \\ $$$${AF}=\sqrt{{r}^{\mathrm{2}} −\left(\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}−\mathrm{2}\right)^{\mathrm{2}} {R}^{\mathrm{2}} } \\ $$$${AF}={R}\sqrt{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${AF}=\frac{\mathrm{1}}{\mathrm{2}}{R}\sqrt{\mathrm{16}\sqrt{\mathrm{2}}−\mathrm{22}} \\ $$$${AB}=\mathrm{2}{AF}=\sqrt{\mathrm{16}\sqrt{\mathrm{2}}−\mathrm{22}}{R}\approx\mathrm{0}.\mathrm{792}{R}\approx\mathrm{4}.\mathrm{753} \\ $$
Commented by cherokeesay last updated on 29/Jul/21
$${I}\:{would}\:{also}\:{like}\:{to}\:{share}\:{my}\:{solution}\:! \\ $$$${thank}\:{you}\:{a}\:{lot}\:{mr}\:{W}\:! \\ $$
Commented by Tawa11 last updated on 29/Jul/21

$$\mathrm{Nice}\:\mathrm{sir}.\:\mathrm{Thanks}. \\ $$
