Question-148540

Question Number 148540 by Jonathanwaweh last updated on 29/Jul/21

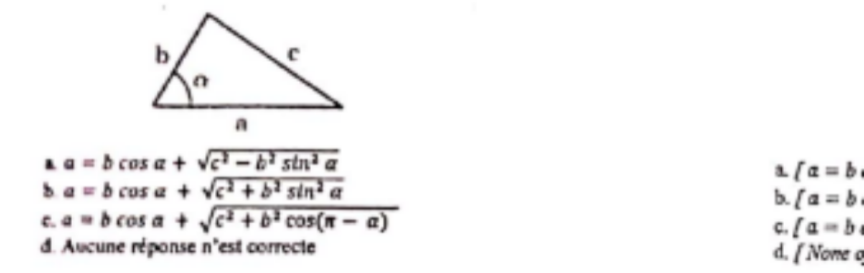
Answered by Olaf_Thorendsen last updated on 29/Jul/21

Formule d′Al−Kashi (generalisation de Pythagore dans un triangle quelconque) : c^2 = a^2 +b^2 −2abcosα ⇒ (a−bcosα)^2 −b^2 cos^2 α+b^2 = c^2 (a−bcosα)^2 +b^2 sin^2 α = c^2 a−bcosα = ±(√(c^2 −b^2 sin^2 α)) On verifie que le bon signe est + avec une valeur particuliere, α = (π/2) par exemple. a−bcosα = (√(c^2 −b^2 sin^2 α)) a = bcosα+(√(c^2 −b^2 sin^2 α)) La bonne reponse est (a).

$$\mathrm{Formule}\:\mathrm{d}'\mathrm{Al}−\mathrm{Kashi}\:\left(\mathrm{generalisation}\right. \\ $$$$\mathrm{de}\:\mathrm{Pythagore}\:\mathrm{dans}\:\mathrm{un}\:\mathrm{triangle} \\ $$$$\left.\mathrm{quelconque}\right)\:: \\ $$$${c}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\alpha \\ $$$$\Rightarrow\:\left({a}−{b}\mathrm{cos}\alpha\right)^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \alpha+{b}^{\mathrm{2}} \:=\:{c}^{\mathrm{2}} \\ $$$$\left({a}−{b}\mathrm{cos}\alpha\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \alpha\:=\:{c}^{\mathrm{2}} \\ $$$${a}−{b}\mathrm{cos}\alpha\:=\:\pm\sqrt{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \alpha} \\ $$$$\mathrm{On}\:\mathrm{verifie}\:\mathrm{que}\:\mathrm{le}\:\mathrm{bon}\:\mathrm{signe}\:\mathrm{est}\:+\:\mathrm{avec} \\ $$$$\mathrm{une}\:\mathrm{valeur}\:\mathrm{particuliere},\:\alpha\:=\:\frac{\pi}{\mathrm{2}}\:\mathrm{par} \\ $$$$\mathrm{exemple}. \\ $$$${a}−{b}\mathrm{cos}\alpha\:=\:\sqrt{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \alpha} \\ $$$$ \\ $$$${a}\:=\:{b}\mathrm{cos}\alpha+\sqrt{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \alpha} \\ $$$$\mathrm{La}\:\mathrm{bonne}\:\mathrm{reponse}\:\mathrm{est}\:\left(\mathrm{a}\right). \\ $$

Facebook Tweet Pin

Question-148540

Leave a Reply Cancel reply