Question Number 148541 by gloriousman last updated on 29/Jul/21

Answered by Olaf_Thorendsen last updated on 29/Jul/21
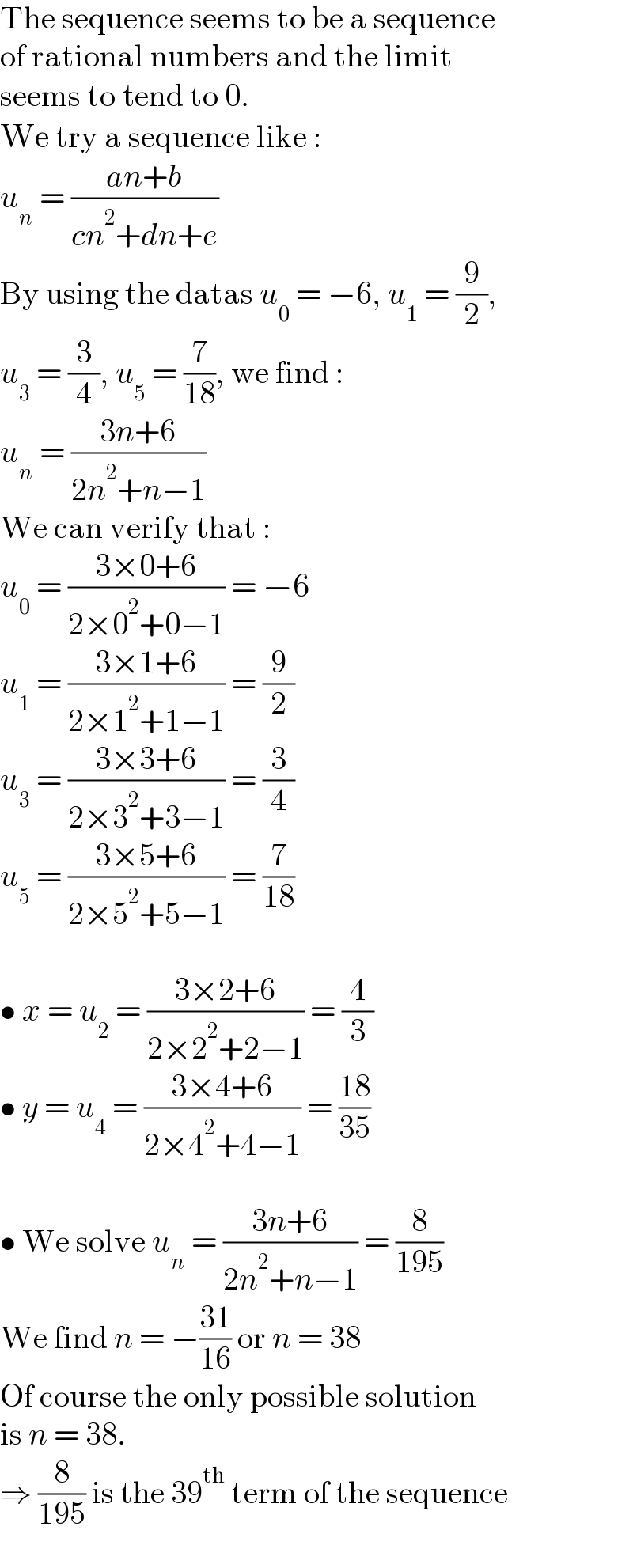
$$\mathrm{The}\:\mathrm{sequence}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{be}\:\mathrm{a}\:\mathrm{sequence} \\ $$$$\mathrm{of}\:\mathrm{rational}\:\mathrm{numbers}\:\mathrm{and}\:\mathrm{the}\:\mathrm{limit} \\ $$$$\mathrm{seems}\:\mathrm{to}\:\mathrm{tend}\:\mathrm{to}\:\mathrm{0}. \\ $$$$\mathrm{We}\:\mathrm{try}\:\mathrm{a}\:\mathrm{sequence}\:\mathrm{like}\:: \\ $$$${u}_{{n}} \:=\:\frac{{an}+{b}}{{cn}^{\mathrm{2}} +{dn}+{e}} \\ $$$$\mathrm{By}\:\mathrm{using}\:\mathrm{the}\:\mathrm{datas}\:{u}_{\mathrm{0}} \:=\:−\mathrm{6},\:{u}_{\mathrm{1}} \:=\:\frac{\mathrm{9}}{\mathrm{2}}, \\ $$$${u}_{\mathrm{3}} \:=\:\frac{\mathrm{3}}{\mathrm{4}},\:{u}_{\mathrm{5}} \:=\:\frac{\mathrm{7}}{\mathrm{18}},\:\mathrm{we}\:\mathrm{find}\:: \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{3}{n}+\mathrm{6}}{\mathrm{2}{n}^{\mathrm{2}} +{n}−\mathrm{1}} \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{verify}\:\mathrm{that}\:: \\ $$$${u}_{\mathrm{0}} \:=\:\frac{\mathrm{3}×\mathrm{0}+\mathrm{6}}{\mathrm{2}×\mathrm{0}^{\mathrm{2}} +\mathrm{0}−\mathrm{1}}\:=\:−\mathrm{6} \\ $$$${u}_{\mathrm{1}} \:=\:\frac{\mathrm{3}×\mathrm{1}+\mathrm{6}}{\mathrm{2}×\mathrm{1}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${u}_{\mathrm{3}} \:=\:\frac{\mathrm{3}×\mathrm{3}+\mathrm{6}}{\mathrm{2}×\mathrm{3}^{\mathrm{2}} +\mathrm{3}−\mathrm{1}}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${u}_{\mathrm{5}} \:=\:\frac{\mathrm{3}×\mathrm{5}+\mathrm{6}}{\mathrm{2}×\mathrm{5}^{\mathrm{2}} +\mathrm{5}−\mathrm{1}}\:=\:\frac{\mathrm{7}}{\mathrm{18}} \\ $$$$ \\ $$$$\bullet\:{x}\:=\:{u}_{\mathrm{2}} \:=\:\frac{\mathrm{3}×\mathrm{2}+\mathrm{6}}{\mathrm{2}×\mathrm{2}^{\mathrm{2}} +\mathrm{2}−\mathrm{1}}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\bullet\:{y}\:=\:{u}_{\mathrm{4}} \:=\:\frac{\mathrm{3}×\mathrm{4}+\mathrm{6}}{\mathrm{2}×\mathrm{4}^{\mathrm{2}} +\mathrm{4}−\mathrm{1}}\:=\:\frac{\mathrm{18}}{\mathrm{35}} \\ $$$$ \\ $$$$\bullet\:\mathrm{We}\:\mathrm{solve}\:{u}_{{n}} \:=\:\frac{\mathrm{3}{n}+\mathrm{6}}{\mathrm{2}{n}^{\mathrm{2}} +{n}−\mathrm{1}}\:=\:\frac{\mathrm{8}}{\mathrm{195}} \\ $$$$\mathrm{We}\:\mathrm{find}\:{n}\:=\:−\frac{\mathrm{31}}{\mathrm{16}}\:\mathrm{or}\:{n}\:=\:\mathrm{38} \\ $$$$\mathrm{Of}\:\mathrm{course}\:\mathrm{the}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{solution} \\ $$$$\mathrm{is}\:{n}\:=\:\mathrm{38}. \\ $$$$\Rightarrow\:\frac{\mathrm{8}}{\mathrm{195}}\:\mathrm{is}\:\mathrm{the}\:\mathrm{39}^{\mathrm{th}} \:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sequence} \\ $$
