Question-148543

Question Number 148543 by liberty last updated on 29/Jul/21

Answered by Rasheed.Sindhi last updated on 30/Jul/21

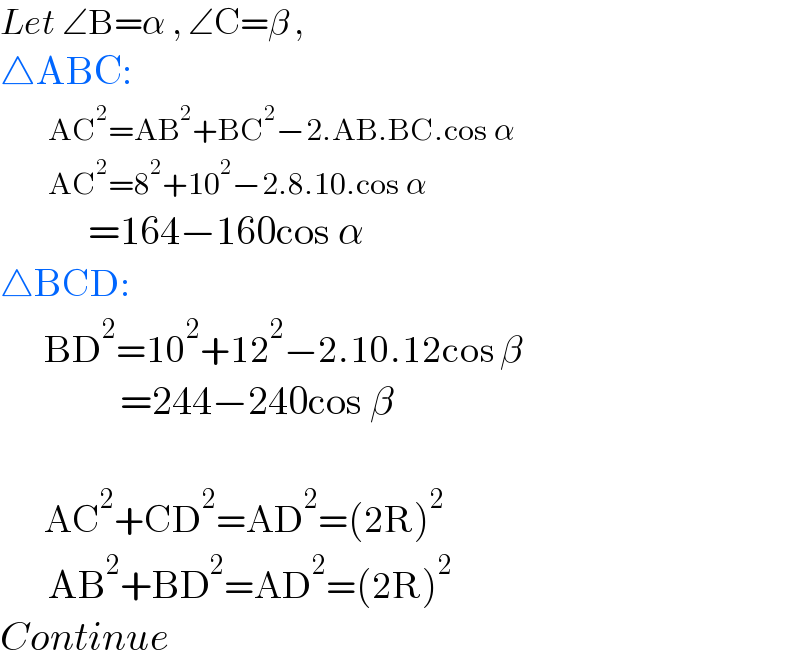
Let ∠B=α , ∠C=β , △ABC: AC^2 =AB^2 +BC^2 −2.AB.BC.cos α AC^2 =8^2 +10^2 −2.8.10.cos α =164−160cos α △BCD: BD^2 =10^2 +12^2 −2.10.12cos β =244−240cos β AC^2 +CD^2 =AD^2 =(2R)^2 AB^2 +BD^2 =AD^2 =(2R)^2 Continue

$${Let}\:\angle\mathrm{B}=\alpha\:,\:\angle\mathrm{C}=\beta\:, \\ $$$$\bigtriangleup\mathrm{ABC}: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{AC}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} +\mathrm{BC}^{\mathrm{2}} −\mathrm{2}.\mathrm{AB}.\mathrm{BC}.\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\mathrm{AC}^{\mathrm{2}} =\mathrm{8}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{2}.\mathrm{8}.\mathrm{10}.\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{164}−\mathrm{160cos}\:\alpha\:\: \\ $$$$\bigtriangleup\mathrm{BCD}: \\ $$$$\:\:\:\:\:\:\:\mathrm{BD}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} −\mathrm{2}.\mathrm{10}.\mathrm{12cos}\:\beta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{244}−\mathrm{240cos}\:\beta \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{AC}^{\mathrm{2}} +\mathrm{CD}^{\mathrm{2}} =\mathrm{AD}^{\mathrm{2}} =\left(\mathrm{2R}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{AB}^{\mathrm{2}} +\mathrm{BD}^{\mathrm{2}} =\mathrm{AD}^{\mathrm{2}} =\left(\mathrm{2R}\right)^{\mathrm{2}} \\ $$$${Continue} \\ $$

Answered by mnjuly1970 last updated on 29/Jul/21

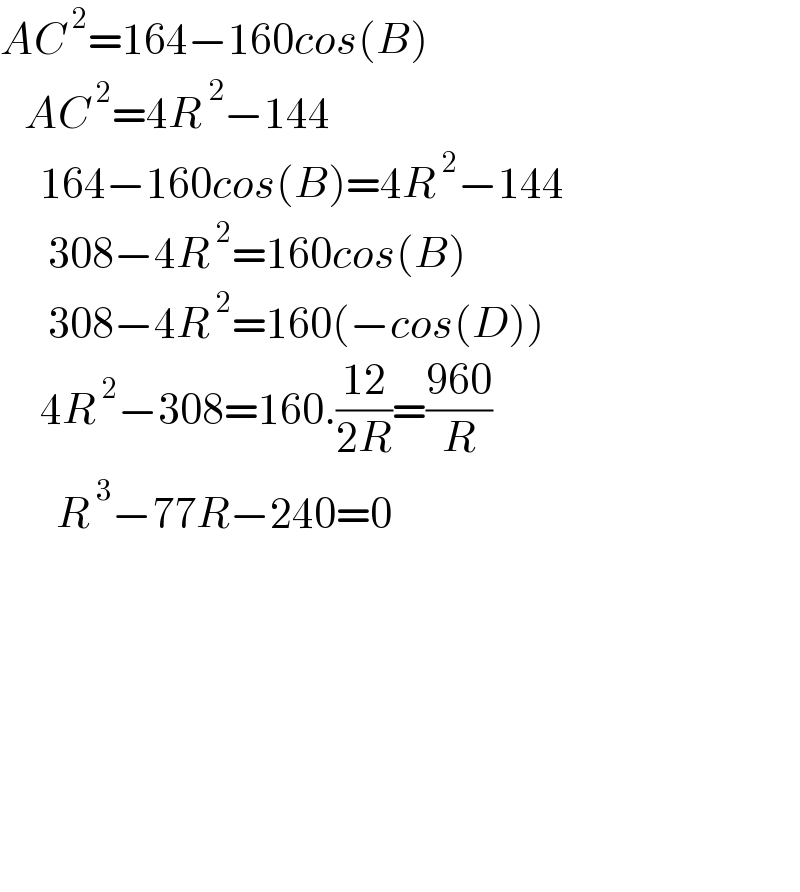
AC^( 2) =164−160cos(B) AC^( 2) =4R^( 2) −144 164−160cos(B)=4R^( 2) −144 308−4R^( 2) =160cos(B) 308−4R^( 2) =160(−cos(D)) 4R^( 2) −308=160.((12)/(2R))=((960)/R) R^( 3) −77R−240=0

$${AC}^{\:\mathrm{2}} =\mathrm{164}−\mathrm{160}{cos}\left({B}\right) \\ $$$$\:\:\:{AC}^{\:\mathrm{2}} =\mathrm{4}{R}^{\:\mathrm{2}} −\mathrm{144} \\ $$$$\:\:\:\:\:\mathrm{164}−\mathrm{160}{cos}\left({B}\right)=\mathrm{4}{R}^{\:\mathrm{2}} −\mathrm{144} \\ $$$$\:\:\:\:\:\:\mathrm{308}−\mathrm{4}{R}^{\:\mathrm{2}} =\mathrm{160}{cos}\left({B}\right) \\ $$$$\:\:\:\:\:\:\mathrm{308}−\mathrm{4}{R}^{\:\mathrm{2}} =\mathrm{160}\left(−{cos}\left({D}\right)\right) \\ $$$$\:\:\:\:\:\mathrm{4}{R}^{\:\mathrm{2}} −\mathrm{308}=\mathrm{160}.\frac{\mathrm{12}}{\mathrm{2}{R}}=\frac{\mathrm{960}}{{R}} \\ $$$$\:\:\:\:\:\:\:{R}^{\:\mathrm{3}} −\mathrm{77}{R}−\mathrm{240}=\mathrm{0} \\ $$$$ \\ $$$$\: \\ $$$$\:\:\: \\ $$$$\:\:\: \\ $$$$ \\ $$$$\:\:\: \\ $$

Answered by mr W last updated on 29/Jul/21

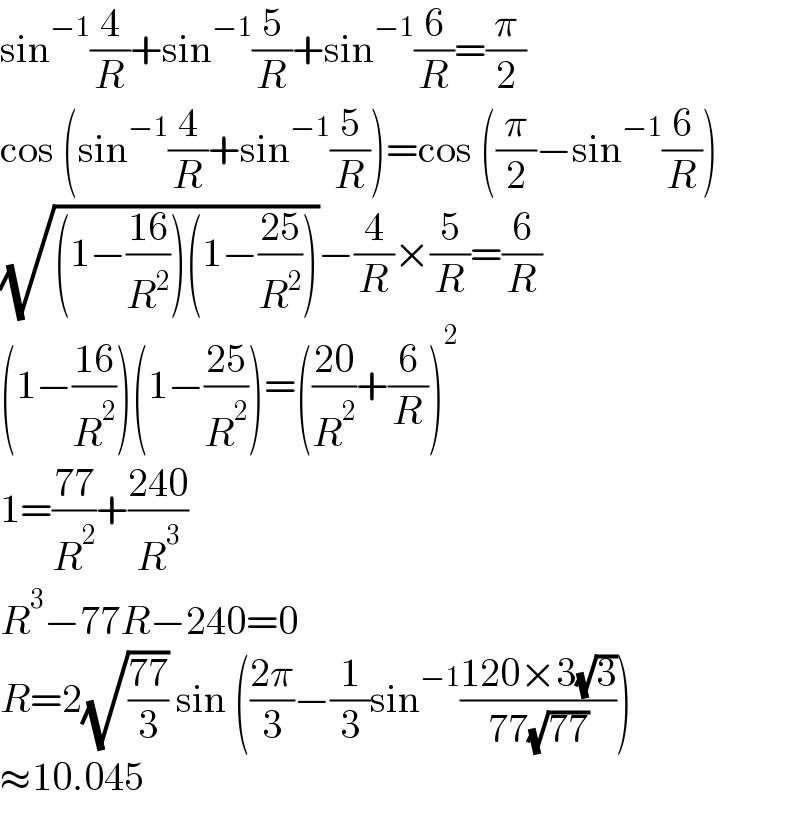
sin^(−1) (4/R)+sin^(−1) (5/R)+sin^(−1) (6/R)=(π/2) cos (sin^(−1) (4/R)+sin^(−1) (5/R))=cos ((π/2)−sin^(−1) (6/R)) (√((1−((16)/R^2 ))(1−((25)/R^2 ))))−(4/R)×(5/R)=(6/R) (1−((16)/R^2 ))(1−((25)/R^2 ))=(((20)/R^2 )+(6/R))^2 1=((77)/R^2 )+((240)/R^3 ) R^3 −77R−240=0 R=2(√((77)/3)) sin (((2π)/3)−(1/3)sin^(−1) ((120×3(√3))/(77(√(77))))) ≈10.045

$$\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{6}}{{R}}=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{{R}}\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{6}}{{R}}\right) \\ $$$$\sqrt{\left(\mathrm{1}−\frac{\mathrm{16}}{{R}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{25}}{{R}^{\mathrm{2}} }\right)}−\frac{\mathrm{4}}{{R}}×\frac{\mathrm{5}}{{R}}=\frac{\mathrm{6}}{{R}} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{16}}{{R}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{25}}{{R}^{\mathrm{2}} }\right)=\left(\frac{\mathrm{20}}{{R}^{\mathrm{2}} }+\frac{\mathrm{6}}{{R}}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}=\frac{\mathrm{77}}{{R}^{\mathrm{2}} }+\frac{\mathrm{240}}{{R}^{\mathrm{3}} } \\ $$$${R}^{\mathrm{3}} −\mathrm{77}{R}−\mathrm{240}=\mathrm{0} \\ $$$${R}=\mathrm{2}\sqrt{\frac{\mathrm{77}}{\mathrm{3}}}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{120}×\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{77}\sqrt{\mathrm{77}}}\right) \\ $$$$\approx\mathrm{10}.\mathrm{045} \\ $$

Commented by liberty last updated on 30/Jul/21

$$\mathrm{great} \\ $$

Answered by mr W last updated on 29/Jul/21

an other way: AC=(√(4R^2 −12^2 )) BD=(√(4R^2 −8^2 )) ABCD is cyclic, therefore AC×BD=AB×CD+BC×AD ⇒(4R^2 −12^2 )(4R^2 −8^2 )=(8×12+20R)^2 ⇒R^3 −77R−240=0 ......

$${an}\:{other}\:{way}: \\ $$$${AC}=\sqrt{\mathrm{4}{R}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} } \\ $$$${BD}=\sqrt{\mathrm{4}{R}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} } \\ $$$${ABCD}\:{is}\:{cyclic},\:{therefore} \\ $$$${AC}×{BD}={AB}×{CD}+{BC}×{AD} \\ $$$$\Rightarrow\left(\mathrm{4}{R}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} \right)\left(\mathrm{4}{R}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} \right)=\left(\mathrm{8}×\mathrm{12}+\mathrm{20}{R}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}^{\mathrm{3}} −\mathrm{77}{R}−\mathrm{240}=\mathrm{0} \\ $$$$…… \\ $$

Commented by Tawa11 last updated on 03/Aug/21

$$\mathrm{Great} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply