Question Number 148768 by mim24 last updated on 31/Jul/21
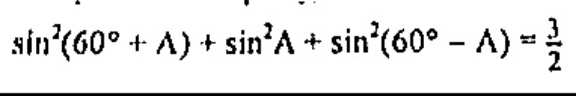
Answered by liberty last updated on 31/Jul/21
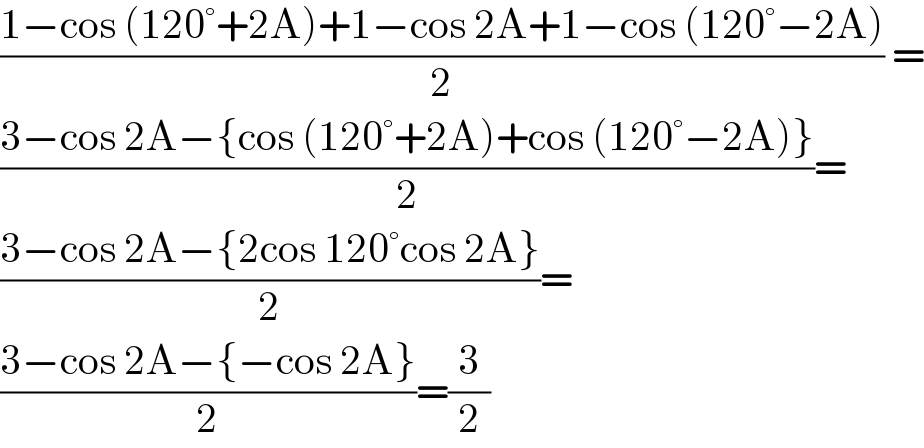
$$\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{120}°+\mathrm{2A}\right)+\mathrm{1}−\mathrm{cos}\:\mathrm{2A}+\mathrm{1}−\mathrm{cos}\:\left(\mathrm{120}°−\mathrm{2A}\right)}{\mathrm{2}}\:= \\ $$$$\frac{\mathrm{3}−\mathrm{cos}\:\mathrm{2A}−\left\{\mathrm{cos}\:\left(\mathrm{120}°+\mathrm{2A}\right)+\mathrm{cos}\:\left(\mathrm{120}°−\mathrm{2A}\right)\right\}}{\mathrm{2}}= \\ $$$$\frac{\mathrm{3}−\mathrm{cos}\:\mathrm{2A}−\left\{\mathrm{2cos}\:\mathrm{120}°\mathrm{cos}\:\mathrm{2A}\right\}}{\mathrm{2}}= \\ $$$$\frac{\mathrm{3}−\mathrm{cos}\:\mathrm{2A}−\left\{−\mathrm{cos}\:\mathrm{2A}\right\}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
