Question Number 148776 by liberty last updated on 31/Jul/21

Answered by mathmax by abdo last updated on 31/Jul/21
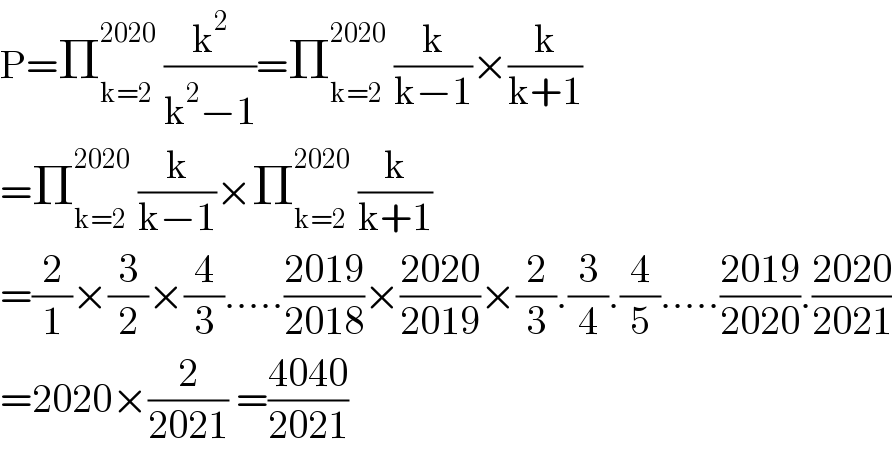
$$\mathrm{P}=\prod_{\mathrm{k}=\mathrm{2}} ^{\mathrm{2020}} \:\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}=\prod_{\mathrm{k}=\mathrm{2}} ^{\mathrm{2020}} \:\frac{\mathrm{k}}{\mathrm{k}−\mathrm{1}}×\frac{\mathrm{k}}{\mathrm{k}+\mathrm{1}} \\ $$$$=\prod_{\mathrm{k}=\mathrm{2}} ^{\mathrm{2020}} \:\frac{\mathrm{k}}{\mathrm{k}−\mathrm{1}}×\prod_{\mathrm{k}=\mathrm{2}} ^{\mathrm{2020}} \:\frac{\mathrm{k}}{\mathrm{k}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}}×\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}…..\frac{\mathrm{2019}}{\mathrm{2018}}×\frac{\mathrm{2020}}{\mathrm{2019}}×\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{4}}{\mathrm{5}}…..\frac{\mathrm{2019}}{\mathrm{2020}}.\frac{\mathrm{2020}}{\mathrm{2021}} \\ $$$$=\mathrm{2020}×\frac{\mathrm{2}}{\mathrm{2021}}\:=\frac{\mathrm{4040}}{\mathrm{2021}} \\ $$
Commented by liberty last updated on 31/Jul/21

$$\mathrm{nice}\:\mathrm{sir} \\ $$
