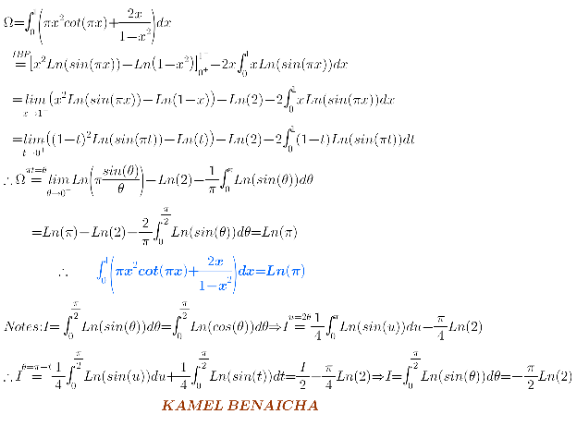Question-148780

Question Number 148780 by Jonathanwaweh last updated on 31/Jul/21

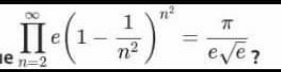
Answered by Kamel last updated on 31/Jul/21

Ω=Π_(n=2) ^(+∞) e(1−(1/n^2 ))^n^2 =e^(Σ_(n=2) ^(+∞) (n^2 Ln(1−(1/n^2 ))+1)) =e^(Σ_(n=2) ^(+∞) n^2 (−Σ_(p=1) ^(+∞) (1/p)(1/n^(2p) )+(1/n^2 ))) =e^(−Σ_(p=1) ^(+∞) (1/(p+1))Σ_(n=2) ^(+∞) (1/n^(2p) )) =e^(−Σ_(p=1) ^(+∞) (1/(p+1))(ζ(2p)−1)) We have: Σ_(k=0) ^(+∞) ζ(2k)x^(2k) =−((πx)/2)cot(πx) So Σ_(k=0) ^(+∞) (ζ(2k)−1)x^(2k+1) =−((πx^2 )/2)cot(πx)−(x/(1−x^2 )) ∴ Σ_(p=0) ^(+∞) ((ζ(2p)−1)/(p+1))=−∫_0 ^1 (πx^2 cot(πx)+((2x)/(1−x^2 )))dx ∫(x^2 cot(πx)+((2x)/(1−x^2 )))dx=((ixLi_2 (e^(−2πix) ))/π^2 )+((Li_3 (e^(−2πix) ))/(2π^3 ))−((ix^3 )/π)+((x^2 Ln(1−e^(2πix) )−πLn(1−x^2 ))/π) ∴ ∫_0 ^1 (πx^2 cot(πx)+((2x)/(1−x^2 )))dx=Ln(π) So: Σ_(p=1) ^(+∞) ((ζ(2p)−1)/(p+1))=(3/2)−Ln(π) Then: 𝚷_(n=2) ^(+∞) e(1−(1/n^2 ))^n^2 =e^(Ln(𝛑)−(3/2)) =(𝛑/(e(√e))) KAMEL BENAICHA

$$ \\ $$$$\Omega=\underset{{n}=\mathrm{2}} {\overset{+\infty} {\prod}}{e}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)^{{n}^{\mathrm{2}} } ={e}^{\underset{{n}=\mathrm{2}} {\overset{+\infty} {\sum}}\left({n}^{\mathrm{2}} {Ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)+\mathrm{1}\right)} \\ $$$$\:\:\:={e}^{\underset{{n}=\mathrm{2}} {\overset{+\infty} {\sum}}{n}^{\mathrm{2}} \left(−\underset{{p}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{p}}\frac{\mathrm{1}}{{n}^{\mathrm{2}{p}} }+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)} ={e}^{−\underset{{p}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{p}+\mathrm{1}}\underset{{n}=\mathrm{2}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}{p}} }} ={e}^{−\underset{{p}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{p}+\mathrm{1}}\left(\zeta\left(\mathrm{2}{p}\right)−\mathrm{1}\right)} \\ $$$${We}\:{have}:\:\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\zeta\left(\mathrm{2}{k}\right){x}^{\mathrm{2}{k}} =−\frac{\pi{x}}{\mathrm{2}}{cot}\left(\pi{x}\right) \\ $$$${So}\:\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(\zeta\left(\mathrm{2}{k}\right)−\mathrm{1}\right){x}^{\mathrm{2}{k}+\mathrm{1}} =−\frac{\pi{x}^{\mathrm{2}} }{\mathrm{2}}{cot}\left(\pi{x}\right)−\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\therefore\:\:\underset{{p}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{p}\right)−\mathrm{1}}{{p}+\mathrm{1}}=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\pi{x}^{\mathrm{2}} {cot}\left(\pi{x}\right)+\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx} \\ $$$$\int\left({x}^{\mathrm{2}} {cot}\left(\pi{x}\right)+\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx}=\frac{{ixLi}_{\mathrm{2}} \left({e}^{−\mathrm{2}\pi{ix}} \right)}{\pi^{\mathrm{2}} }+\frac{{Li}_{\mathrm{3}} \left({e}^{−\mathrm{2}\pi{ix}} \right)}{\mathrm{2}\pi^{\mathrm{3}} }−\frac{{ix}^{\mathrm{3}} }{\pi}+\frac{{x}^{\mathrm{2}} {Ln}\left(\mathrm{1}−{e}^{\mathrm{2}\pi{ix}} \right)−\pi{Ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\pi} \\ $$$$\therefore\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\pi{x}^{\mathrm{2}} {cot}\left(\pi{x}\right)+\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx}={Ln}\left(\pi\right) \\ $$$${So}:\:\underset{{p}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{p}\right)−\mathrm{1}}{{p}+\mathrm{1}}=\frac{\mathrm{3}}{\mathrm{2}}−{Ln}\left(\pi\right) \\ $$$${Then}:\:\:\:\:\:\:\:\:\:\:\:\underset{\boldsymbol{{n}}=\mathrm{2}} {\overset{+\infty} {\boldsymbol{\prod}}{e}}\left(\mathrm{1}−\frac{\mathrm{1}}{\boldsymbol{{n}}^{\mathrm{2}} }\right)^{\boldsymbol{{n}}^{\mathrm{2}} } =\boldsymbol{{e}}^{\boldsymbol{{Ln}}\left(\boldsymbol{\pi}\right)−\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\boldsymbol{\pi}}{\boldsymbol{{e}}\sqrt{\boldsymbol{{e}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{KAMEL}}\:\boldsymbol{{BENAICHA}} \\ $$

Commented by Tawa11 last updated on 02/Aug/21

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Answered by Kamel last updated on 31/Jul/21

Facebook Tweet Pin

Leave a Reply Cancel reply