Question Number 148783 by 0731619 last updated on 31/Jul/21
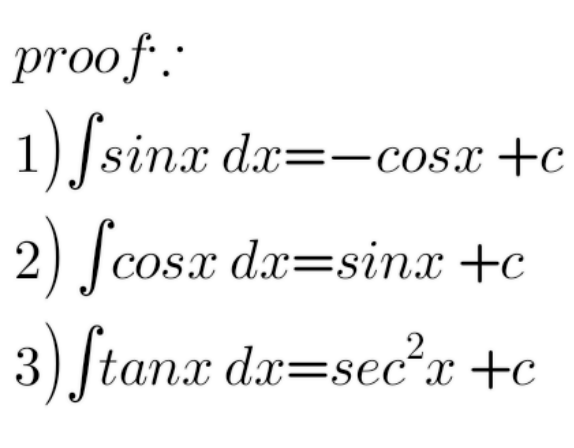
Commented by hknkrc46 last updated on 31/Jul/21
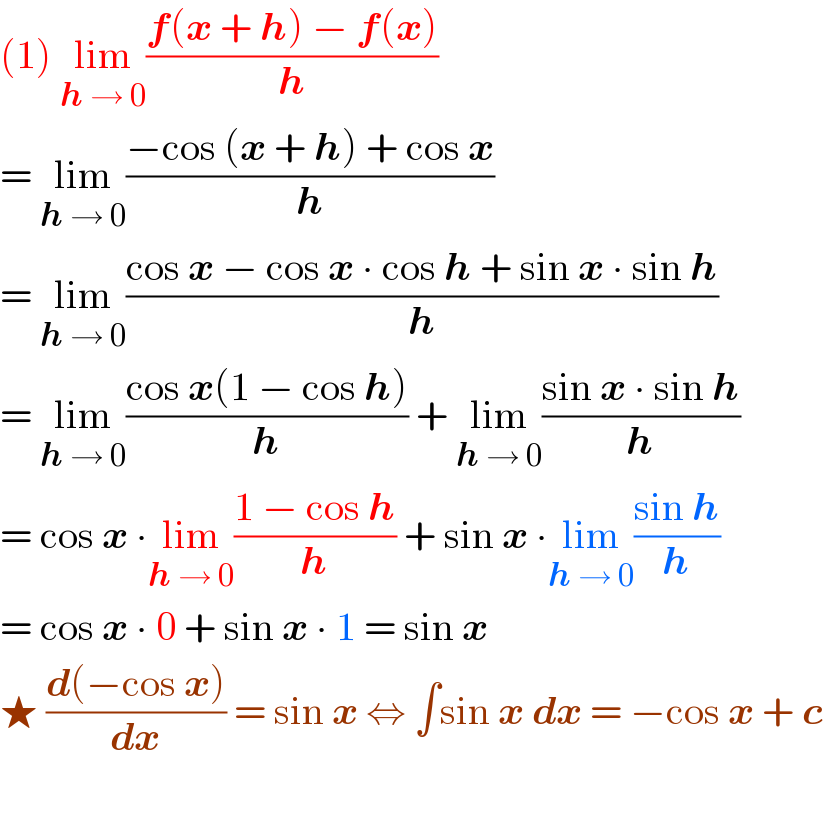
$$\left(\mathrm{1}\right)\:\underset{\boldsymbol{{h}}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{f}}\left(\boldsymbol{{x}}\:+\:\boldsymbol{{h}}\right)\:−\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{h}}}\: \\ $$$$=\:\underset{\boldsymbol{{h}}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{cos}\:\left(\boldsymbol{{x}}\:+\:\boldsymbol{{h}}\right)\:+\:\mathrm{cos}\:\boldsymbol{{x}}}{\boldsymbol{{h}}} \\ $$$$=\:\underset{\boldsymbol{{h}}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\boldsymbol{{x}}\:−\:\mathrm{cos}\:\boldsymbol{{x}}\:\centerdot\:\mathrm{cos}\:\boldsymbol{{h}}\:+\:\mathrm{sin}\:\boldsymbol{{x}}\:\centerdot\:\mathrm{sin}\:\boldsymbol{{h}}}{\boldsymbol{{h}}} \\ $$$$=\:\underset{\boldsymbol{{h}}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\boldsymbol{{x}}\left(\mathrm{1}\:−\:\mathrm{cos}\:\boldsymbol{{h}}\right)}{\boldsymbol{{h}}}\:+\:\underset{\boldsymbol{{h}}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\boldsymbol{{x}}\:\centerdot\:\mathrm{sin}\:\boldsymbol{{h}}}{\boldsymbol{{h}}} \\ $$$$=\:\mathrm{cos}\:\boldsymbol{{x}}\:\centerdot\underset{\boldsymbol{{h}}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}\:−\:\mathrm{cos}\:\boldsymbol{{h}}}{\boldsymbol{{h}}}\:+\:\mathrm{sin}\:\boldsymbol{{x}}\:\centerdot\underset{\boldsymbol{{h}}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\boldsymbol{{h}}}{\boldsymbol{{h}}} \\ $$$$=\:\mathrm{cos}\:\boldsymbol{{x}}\:\centerdot\:\mathrm{0}\:+\:\mathrm{sin}\:\boldsymbol{{x}}\:\centerdot\:\mathrm{1}\:=\:\mathrm{sin}\:\boldsymbol{{x}} \\ $$$$\bigstar\:\frac{\boldsymbol{{d}}\left(−\mathrm{cos}\:\boldsymbol{{x}}\right)}{\boldsymbol{{dx}}}\:=\:\mathrm{sin}\:\boldsymbol{{x}}\:\Leftrightarrow\:\int\mathrm{sin}\:\boldsymbol{{x}}\:\boldsymbol{{dx}}\:=\:−\mathrm{cos}\:\boldsymbol{{x}}\:+\:\boldsymbol{{c}} \\ $$$$\: \\ $$
