Question Number 148797 by kameda last updated on 31/Jul/21
Answered by puissant last updated on 31/Jul/21

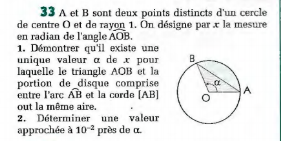
$$\left.\mathrm{1}\right) \\ $$$$\mathrm{sin}\alpha=\frac{\mathrm{AB}}{\mathrm{OA}}\:\Rightarrow\:\mathrm{sin}\alpha=\frac{\mathrm{AB}}{\mathrm{1}}\:\mathrm{car}\:\mathrm{c}'\mathrm{est}\:\mathrm{un} \\ $$$$\mathrm{cercle}\:\mathrm{de}\:\mathrm{rayon}\:\mathrm{1}.. \\ $$$$\Rightarrow\mathrm{AB}=\mathrm{sin}\left(\mathrm{x}\right)\:\mathrm{car}\:\alpha\:\mathrm{est}\:\mathrm{represent}\acute {\mathrm{e}}\:\mathrm{par}\:\mathrm{x}. \\ $$$$\mathrm{A}_{\Delta} =\frac{\mathrm{AB}×\mathrm{h}}{\mathrm{2}}\:=\:\frac{\mathrm{AB}}{\mathrm{2}}\:=\:\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{2}}..\:\mathrm{car}\:\mathrm{h}=\mathrm{1} \\ $$$$\mathrm{D}'\mathrm{autre}\:\mathrm{part},\:\mathrm{l}'\mathrm{air}\:\mathrm{de}\:\mathrm{l}'\mathrm{arc}\:\mathrm{AB}\:\mathrm{est}:\: \\ $$$$\mathrm{A}_{\mathrm{l}'\mathrm{arc}} +\mathrm{A}_{\bigtriangleup} =\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{A}_{\mathrm{l}'\mathrm{arc}} =\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{A}_{\bigtriangleup} =\frac{\mathrm{x}}{\mathrm{2}}−\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{2}}.. \\ $$$$\mathrm{Alors}\:,\:\mathrm{pour}\:\mathrm{que}\:\mathrm{A}_{\mathrm{l}'\mathrm{arc}} =\mathrm{A}_{\bigtriangleup} ,\:\mathrm{il}\:\mathrm{faut}\:\mathrm{que}: \\ $$$$\mathrm{A}_{\bigtriangleup} −\mathrm{A}_{\mathrm{l}'\mathrm{arc}} =\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{sin}\left(\mathrm{x}\right)−\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{posons}\:\mathrm{A}\left(\mathrm{x}\right)=\mathrm{sin}\left(\mathrm{x}\right)−\frac{\mathrm{x}}{\mathrm{2}}.. \\ $$$$\mathrm{etudier}\:\mathrm{la}\:\mathrm{fonction}\:\mathrm{et}\:\mathrm{trouver}\:\mathrm{l}'\mathrm{intervalle} \\ $$$$\mathrm{ou}\:\mathrm{la}\:\mathrm{variable}\:\mathrm{se}\:\mathrm{trouve}.. \\ $$$$\left.\mathrm{2}\right) \\ $$$$….\mathrm{Trivial}.. \\ $$
