Menu Close

Question-148798

Tinku Tara 0 Comments
Pin




Question Number 148798 by abdurehime last updated on 31/Jul/21
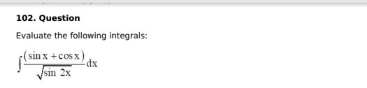
Answered by puissant last updated on 31/Jul/21
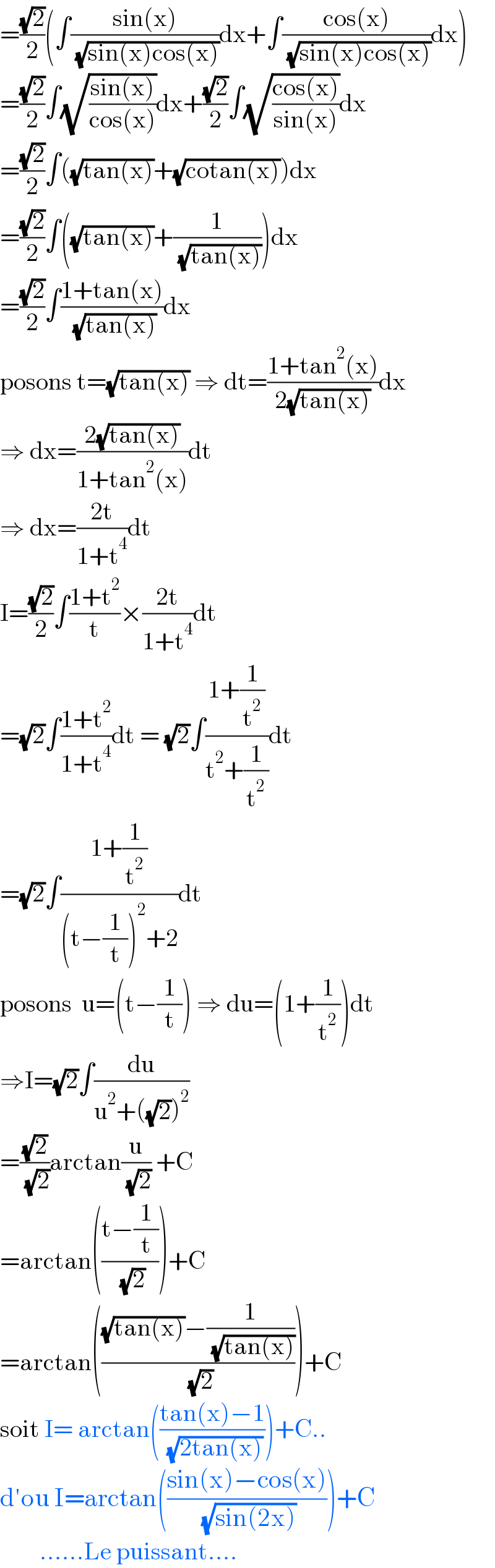
=((√2)/2)(∫((sin(x))/( (√(sin(x)cos(x)))))dx+∫((cos(x))/( (√(sin(x)cos(x)))))dx) =((√2)/2)∫(√((sin(x))/(cos(x))))dx+((√2)/2)∫(√((cos(x))/(sin(x))))dx =((√2)/2)∫((√(tan(x)))+(√(cotan(x))))dx =((√2)/2)∫((√(tan(x)))+(1/( (√(tan(x))))))dx =((√2)/2)∫((1+tan(x))/( (√(tan(x)))))dx posons t=(√(tan(x))) ⇒ dt=((1+tan^2 (x))/(2(√(tan(x)))))dx ⇒ dx=((2(√(tan(x))))/(1+tan^2 (x)))dt ⇒ dx=((2t)/(1+t^4 ))dt I=((√2)/2)∫((1+t^2 )/t)×((2t)/(1+t^4 ))dt =(√2)∫((1+t^2 )/(1+t^4 ))dt = (√2)∫((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt =(√2)∫((1+(1/t^2 ))/((t−(1/t))^2 +2))dt posons u=(t−(1/t)) ⇒ du=(1+(1/t^2 ))dt ⇒I=(√2)∫(du/(u^2 +((√2))^2 )) =((√2)/( (√2)))arctan(u/( (√2))) +C =arctan(((t−(1/t))/( (√2))))+C =arctan((((√(tan(x)))−(1/( (√(tan(x))))))/( (√2))))+C soit I= arctan(((tan(x)−1)/( (√(2tan(x))))))+C.. d′ou I=arctan(((sin(x)−cos(x))/( (√(sin(2x))))))+C ......Le puissant....
$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\int\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)}}\mathrm{dx}+\int\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)}}\mathrm{dx}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\sqrt{\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{cos}\left(\mathrm{x}\right)}}\mathrm{dx}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\sqrt{\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{sin}\left(\mathrm{x}\right)}}\mathrm{dx} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\left(\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}+\sqrt{\mathrm{cotan}\left(\mathrm{x}\right)}\right)\mathrm{dx} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\left(\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}}\right)\mathrm{dx} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{\mathrm{1}+\mathrm{tan}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}}\mathrm{dx} \\ $$$$\mathrm{posons}\:\mathrm{t}=\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}\:\Rightarrow\:\mathrm{dt}=\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{2}\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}}\mathrm{dx} \\ $$$$\Rightarrow\:\mathrm{dx}=\frac{\mathrm{2}\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dt} \\ $$$$\Rightarrow\:\mathrm{dx}=\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$$$\mathrm{I}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{t}}×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$$$=\sqrt{\mathrm{2}}\int\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt}\:=\:\sqrt{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt} \\ $$$$=\sqrt{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt} \\ $$$$\mathrm{posons}\:\:\mathrm{u}=\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)\:\Rightarrow\:\mathrm{du}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$\Rightarrow\mathrm{I}=\sqrt{\mathrm{2}}\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\frac{\mathrm{u}}{\:\sqrt{\mathrm{2}}}\:+\mathrm{C} \\ $$$$=\mathrm{arctan}\left(\frac{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C} \\ $$$$=\mathrm{arctan}\left(\frac{\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\left(\mathrm{x}\right)}}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C} \\ $$$$\mathrm{soit}\:\mathrm{I}=\:\mathrm{arctan}\left(\frac{\mathrm{tan}\left(\mathrm{x}\right)−\mathrm{1}}{\:\sqrt{\mathrm{2tan}\left(\mathrm{x}\right)}}\right)+\mathrm{C}.. \\ $$$$\mathrm{d}'\mathrm{ou}\:\mathrm{I}=\mathrm{arctan}\left(\frac{\mathrm{sin}\left(\mathrm{x}\right)−\mathrm{cos}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{sin}\left(\mathrm{2x}\right)}}\right)+\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:……\mathrm{Le}\:\mathrm{puissant}…. \\ $$
Commented by abdurehime last updated on 31/Jul/21
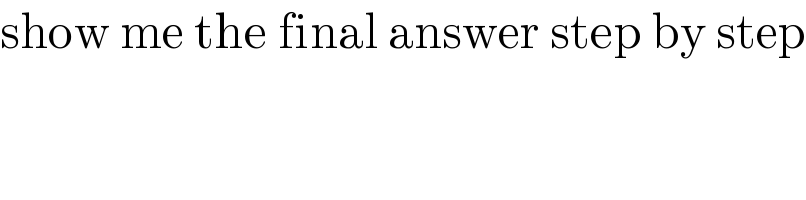
show me the final answer step by step
$$\mathrm{show}\:\mathrm{me}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step} \\ $$
Answered by Kamel last updated on 31/Jul/21
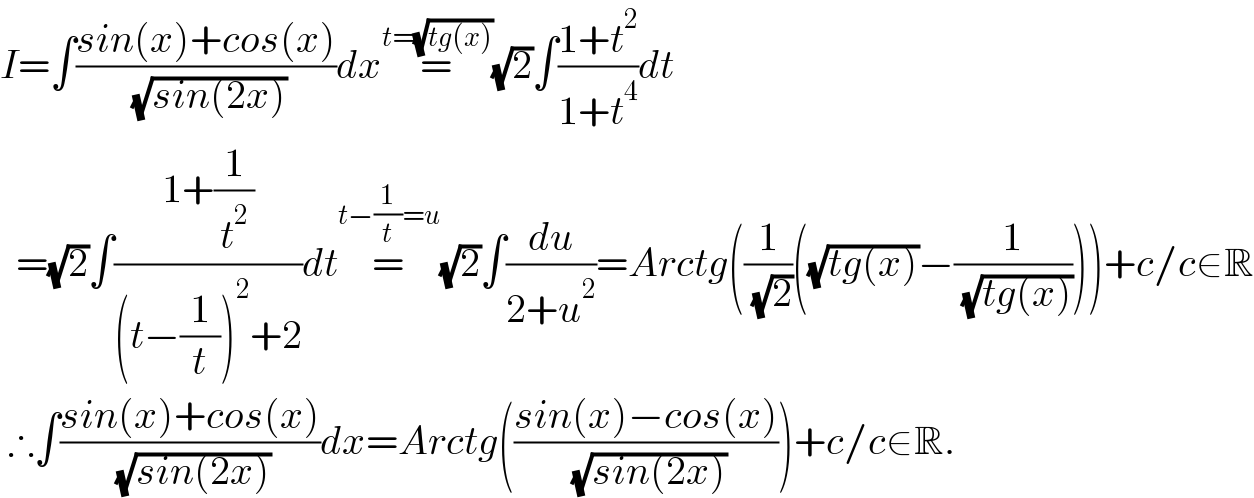
I=∫((sin(x)+cos(x))/( (√(sin(2x)))))dx=^(t=(√(tg(x)))) (√2)∫((1+t^2 )/(1+t^4 ))dt =(√2)∫((1+(1/t^2 ))/((t−(1/t))^2 +2))dt=^(t−(1/t)=u) (√2)∫(du/(2+u^2 ))=Arctg((1/( (√2)))((√(tg(x)))−(1/( (√(tg(x)))))))+c/c∈R ∴∫((sin(x)+cos(x))/( (√(sin(2x)))))dx=Arctg(((sin(x)−cos(x))/( (√(sin(2x))))))+c/c∈R.
$${I}=\int\frac{{sin}\left({x}\right)+{cos}\left({x}\right)}{\:\sqrt{{sin}\left(\mathrm{2}{x}\right)}}{dx}\overset{{t}=\sqrt{{tg}\left({x}\right)}} {=}\sqrt{\mathrm{2}}\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$$\:\:=\sqrt{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}}{dt}\overset{{t}−\frac{\mathrm{1}}{{t}}={u}} {=}\sqrt{\mathrm{2}}\int\frac{{du}}{\mathrm{2}+{u}^{\mathrm{2}} }={Arctg}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\sqrt{{tg}\left({x}\right)}−\frac{\mathrm{1}}{\:\sqrt{{tg}\left({x}\right)}}\right)\right)+{c}/{c}\in\mathbb{R} \\ $$$$\:\therefore\int\frac{{sin}\left({x}\right)+{cos}\left({x}\right)}{\:\sqrt{{sin}\left(\mathrm{2}{x}\right)}}{dx}={Arctg}\left(\frac{{sin}\left({x}\right)−{cos}\left({x}\right)}{\:\sqrt{{sin}\left(\mathrm{2}{x}\right)}}\right)+{c}/{c}\in\mathbb{R}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *